Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 9

Considere uma estrela binaria cujos componentes, de massas m 1 e m 2 , separadas por uma distancia r , descrevem orbitas circulares de período t em torno do CM do par. Seja T s o período da orbita da Terra, de raio médio R , em torno do Sol, de massa M s . (a) Mostre que

T T s 2 = M s m 1 + m 2 r R 3

(b) Aplique este resultado para calcular o período da estrela dupla Sirius A – Sirius B, sabendo que a massa de Sirius A é 2,2 M s e a de Sírius B é 0,9 M s . A separação do par é de 19,9   U A . Despreze a excentricidade das órbitas. (c) Calcule os raios r a e r b das órbitas de Sírius A e Sírius B.

Passo 1

Essa situação vai ser assim, ó:

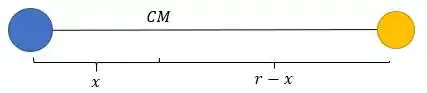
A força resultante no corpo da esquerda é a força gravitacional. Então essa vai ser a centrípeta! Tem que tomar cuidado com a centrípeta, porque ela é com relação ao centro de massa!

m 1 ω 2 x = G m 1 m 2 r 2

ω 2 = G m 2 r 2 x

Bom, agora vamos calcular a posição do centro de massa. Pra isso a gente vai usar aquela fórmulinha clássica!

x = m 2 r m 1 + m 2

Vamos substituir isso ali em cima:

ω 2 = G m 2 r 2 m 2 r m 1 + m 2

ω 2 = G m 1 + m 2 r 3

Passo 2

Beleza, e como a gente chega disso no período? Moleza! É só lembrar que ω = 2 π T !

2 π T 2 = G m 1 + m 2 r 3

4 π 2 T 2 = G m 1 + m 2 r 3

Para o sistema Terra-Sol, vamos usar a terceira lei de Kepler!

4 π 2 T s 2 = G M s R 3

Bom, agora a gente divide as equações pra achar o que queremos:

T T s 2 = M s m 1 + m 2 r R 3

Que é o que a gente queria!

Passo 3

Agora vamos aplicar os valores. A gente tem esses aqui: m 1 + m 2 = 2.2 + 0.9 M s = 3.1 M s e r = 19.9   U A . Além disso, T s = 365   d i a s . Substituindo...

T 365 2 = M s 3.1 M s 19.9 3

T = 1.84 × 10 4   d i a s

T = 50.4   a n o s

Passo 4

Agora a gente consegue calcular os dois raios de órbita mole mole!

r A = r m 2 m 1 + m 2 = 19.9 0.9 3.1 = 5.8   U A

r A + r B = 19.9

r B = 14.1   U A

Resposta

  1. T T s 2 = M s m 1 + m 2 r R 3
  2. T = 50.4   a n o s
  3. r A = 5.8   U A ,   r B = 14.1   U A
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supondo que a atração gravitacional da nossa galáxia, de massa total M g e raio R g , atua como se toda a massa estivesse concentrada no seu centro, e comparando a órbita circular em torno de uma estr
O diâmetro angular aparente do Sol visto da Terra (ângulo subentendido pelo disco solar) é de 0,55 ° . Utilizando apenas estes dados, juntamente com o período da órbita da Terra em torno do Sol, aprox
Uma espaçonave está viajando ao longo da reta que liga o centro da Terra ao centro da Lua. A que distância da Terra a força gravitacional total que a Terra e a Lua exercem sobre a a nave é zero?
Um satélite de 125k g de massa está em uma órbita circular de raio 7,00.10 6m em torno de um planeta. Se o período é 8050s , qual é a energia mecânica do satélite?
Qual é a variação percentual da aceleração percentual da aceleração da Terra em direção ao Sol quando o alinhamento entre a Terra, o Sol e a Lua muda de um eclipse do Sol (com a Lua entre a Terra e o