Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 69

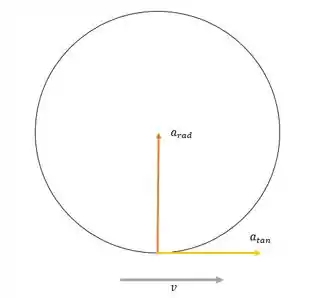
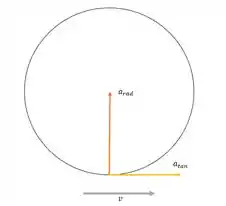
Um automóvel clássico Chevrolet Corvette 1957 com 1240   k g parte do repouso e acelera com aceleração tangencial constante igual a 3,0   m / s 2   em uma pista de teste circular com raio de 60,0   m . Considere o carro como uma partícula. a) Qual é sua aceleração angular? b) Qual é sua velocidade angular 6,0   s depois do início? c) Qual é sua aceleração radial nesse instante? d) Faça um esboço de uma vista do topo mostrando a pista circular, o carro, o vetor velocidade e os componentes do vetor aceleração 6,0 s depois de o carro iniciar o movimento. e) Qual é o módulo da aceleração resultante e da força resultante sobre o carro nesse instante? f) Qual é o ângulo formado entre a velocidade do carro nesse instante e a aceleração resultante e entre a velocidade e a força resultante?

Passo 1

Oi, galerinha!

Temos uma questão com muitos questionamentos. Mas fica tranquilo, que o que faremos aqui basicamente será aplicar fórmulas diretamente com os dados do enunciado. Então vamos relembrar algumas formulinhas!

Temos que a aceleração tangencial é:

a t a n = r α

E a aceleração radial é:

a r a d = r ω 2

E ambas acelerações, a t a n e a a r a d , são componentes perpendiculares, então:

a = a t a n 2 +   a r a d 2

Bora começar!

Passo 2

  1. Para encontrarmos a aceleração angular, vamos utilizar a aceleração tangencial, dessa forma: a t a n = r α

    2. Isso implica que:

    α = a t a n r

    Pelo enunciado temos que: a t a n = 3 m / s 2 r = 60 m

    Então:

    α = 3 m / s 2 60 m = 0,050 r a d / s 2

    Tranquilo até aqui?

    Passo 3

  2. Para calcuarmos a velocidade angular 6 s após o início, basta fazermos:

    3. ω = α t

    ω = 0,050 r a d s 2 ⋅ 6 s

    ω = 0,300 r a d / s

    Bacana, não é?

    Passo 4

  3. Temos que a aceleração radial é dada por:

    4. a r a d = r ω 2

    Isso implica que:

    a r a d = 60 m ⋅ 0,300 r a d s 2

    a r a d = 5,40 m / s 2  

    Show?

    Passo 5

  4. Estamos quase lá!

    Passo 6

  5. Então, o módulo da aceleração resultante e da força resultante sobre o carro será calculada por:

    6. a = a t a n 2 +   a r a d 2

    Temos que: a r a d = 5,40 m / s 2 a t a n = 3 m / s 2

    Assim:

    a = 3 m s 2 2 +   5,40 m s 2 2

    a = 6,18 m / s 2

    Legal?

    Passo 7

  6. E então vamos aplicar a segunda lei de Newton para calcularmos a força, F .

∑ F = m a  

Temos que: a = 6,18 m / s 2 m = 1240   k g

⇒ F = 1240   k g ⋅ 6,18 m s 2

F = 7,66 k N

Está acompanhando?

Passo 3

Para encontrarmos o ângulo, fazemos:

θ = tan - 1 ⁡ a r a d a t a n   = tan - 1 ⁡ 5,40 3

θ = 60,9 °

E aí! O que achou? Responde Aí!

Resposta

  1. α = 0,050 r a d / s 2
  2. α t = 0,300 r a d / s
  3. a r a d = 5,40 m / s 2

  5. a = 6,18 m / s 2 e F = 7,66 k N
  6. θ = 60,9 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um grande rolo de papel de 16,0 kg com raio R =18,0 cm está em repouso contra uma parede e é mantido no lugar por um suporte ligado a uma barra que passa em seu centro (Figura 10.54). A barra pode gir
O motor de uma serra de mesa gira com 3450 rev/min. Uma polia ligada ao eixo do motor movimenta uma segunda polia com metade do diâmetro por meio de uma correia V. Uma serra circular de diâmetro igual
Acorreia de uma máquina de lavar a vácuo é enrolada ligando um eixo de raio igual a 0,45 cm com uma roda de raio igual a 2,0cm. O arranjo envolvendo a correia, o eixo e a roda é semelhante ao descrito
Faça um desenho de uma roda situada no plano do papel e girando no sentido anti-horário. Escolha um ponto sobre a circunferência e desenhe um vetor r → ligando o centro com esse ponto. a) Qual é a dir