Um grande rolo de papel de 16,0 kg com raio R =18,0 cm está em repouso contra uma parede e é mantido no lugar por um suporte ligado a uma barra que passa em seu centro (Figura 10.54). A barra pode girar sem atrito no suporte, e o momento de inércia do papel e da barra em torno do disco é igual a 0,260 . A outra extremidade da barra está presa à parede por uma articulação sem atrito de modo que a barra faz um ângulo de 30,0º com a parede. O peso da barra é desprezível. O coeficiente de atrito cinético entre o papel e a parede é c 0,25. Uma força constante vertical F= 40,0 N é aplicada ao papel, e o papel desenrola.
a) Qual é o módulo da força que a barra exerce sobre o papel enquanto ele desenrola?
b) Qual é a aceleração angular do rolo?
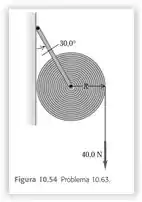
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um grande rolo de papel de com raio está em repouso contra uma parede e é mantido no lugar por um suporte ligado a uma barra que passa em seu centro.
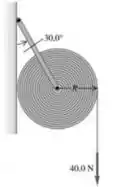
A barra pode girar sem atrito no suporte, e o momento de inércia do papel e da barra em torno do disco é igual a .
A outra extremidade da barra está presa à parede por uma articulação sem atrito de modo que a barra faz um ângulo de com a parede. O peso da barra é desprezível.
O coeficiente de atrito cinético entre o papel e a parede é .
Uma força constante vertical é aplicada ao papel, e o papel desenrola.
Queremos calcular o módulo da força que a barra exerce sobre o papel enquanto ele desenrola.
Para isso, precisaremos da seguinte expressão (Segunda Lei de Newton):
Onde é força, é a massa e é a aceleração.
Também queremos calcular a aceleração angular do rolo. Para isso, precisaremos da seguinte expressão:
Onde é o torque, é o momento angulae e é a aceleração angular.
Passo 2
Analisemos que no ponto de contato, a parede exerce uma força de atrito direcionada para baixo e uma força normal direcionado para a direita.
Essa é uma situação em que a força líquida no rolo é zero, mas o torque líquido não é zero.
Feito isso, precisamos equilibrar as forças verticais e as horizontais, a fim de encontrar o módulo da força que a barra exerce sobre o papel.
No segundo momento, temos que a haste e a força normal exercem torque zero, a partir disso encontraremos a aceleração.
Passo 3
Fazendo a análise das forças...
(vertical)
(horizontal)
Onde é a força peso.
Lembrando que .
Substituindo,
Como , eliminamos o
Assim,
Passo 4
Em segundo, para encontrarmos a aceleração do rolo é só aplicarmos
É importante lembrarmos que quando substituirmos o torque, a magnitude da rede é , e pode ser encontrado pela inserção do valor encontrado para a haste F em uma das relações; ou seja.
Substituindo os dados...
Logo,
Resposta
a)
b)