Faça um desenho de uma roda situada no plano do papel e girando no sentido anti-horário. Escolha um ponto sobre a circunferência e desenhe um vetor ligando o centro com esse ponto. a) Qual é a direção e o sentido de ? b) Mostre que a velocidade desse ponto é dada por . c) Mostre que a aceleração radial desse ponto é dada por). (Veja o Exercício 9.28.)
Passo 1
E aí! Tudo certinho?
Bom, vamos lá. Primeira coisa que a gente vai fazer é o que o enunciado pede: desenhar uma roda situada no plano do papel e girando no sentido anti-horário, e desenhar um vetor que vai do centro até um ponto da roda.
Fica assim:
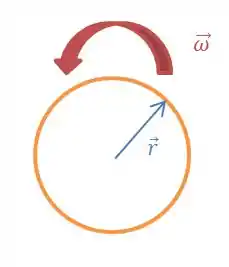
Beleza, isso feito, vamos para a primeira pergunta!
Passo 2
- Aqui queremos a direção e sentido da velocidade angular , e vamos responder isso olhando para figura!
Então, para velocidade angular geralmente a gente fala que ela está no sentido horário ou anti-horário, mas tem uma forma mais “correta” de dar essa direção que é pela regra da mão direita.
Para isso, você precisa abraçar a velocidade angular com os dedos da mão direita na direção da rotação, para onde o seu polegar apontar é a direção da velocidade angular.
Se fizermos isso no caso da nossa roda, vamos ver que o nosso polegar aponta para fora do plano da página.
Por convenção, o eixo é para direita, o para cima e o para fora do plano da página.
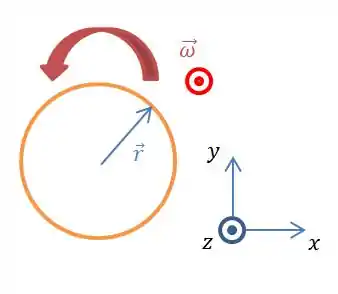
Portanto a nossa velocidade angular está na direção do eixo e no sentido positivo, ou seja, para fora do plano da página.
Tranquilo até aqui?
Passo 3
Vamos verificar para a letra b) se:
Para isso, eu vou desenhar a roda novamente:
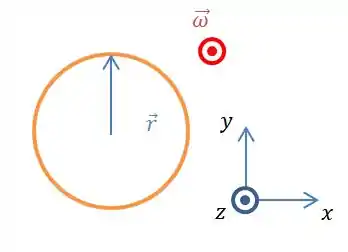
Podemos ver que está na direção do eixo positivo.
E também podemos ver que está no sentido do eixo positivo.
Portanto, se fizermos o produto vetorial, teremos:
O produto vetorial entre é igual a , portanto, temos:
Ou seja, esse produto vetorial dá num vetor que aponta na direção negativa do eixo .
E se olharmos para a nossa figura, no ponto que estamos avaliando a velocidade aponta realmente para essa direção, afinal a roda gira no sentido anti-horário:
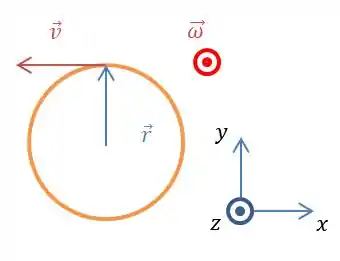
Portanto o vetor velocidade tem a mesma direção que o produto vetorial
Show?
Passo 4
- Como é perpendicular a , então temos que o módulo do produto vetorial é:
Pela Regra da mão direita, o vetor resultante se encontra na direção de .
Analisando as unidades da velocidade angular e velocidade, teremos:
Opa, repara que é unidade de aceleração. Desta forma temos que:
Se a roda girar no sentido horário, as direções de e estão invertidos, mas a ainda está para o centro.
E então! O que achou? Responde Aí!
Resposta
- A velocidade angular está na direção do eixo e no sentido positivo.
- Como demonstrado no Passo 3.
- Como demonstrado no Passo 4.