Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 48
Um automóvel sobe uma ladeira inclinada de a . O coeficiente de atrito estático entre os pneus e a pista é . (a) Qual é a menor distância necessária para o carro parar? (b) Qual seria a menor distância para parar se o carro estivesse descendo a ladeira?
Passo 1
a) Fala, querido! Então, o carro está subindo uma ladeira inclinada e começa a frear, e ele quer a menor distância que ele se desloca depois que aperta o freio até . Vamos resumir nossas informações do movimento num desenho lindão:
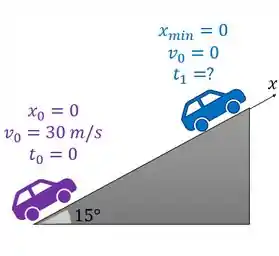
Percebe que isso vai ser um movimento acelerado. Então a gente pode usar as equações de movimento com aceleração constante porque temos forças constantes agindo.
E uma dessas equações é a de Torricelli, onde temos:
Como a velocidade final e , então:
Temos , mas não temos . Precisamos descobrir!
Passo 2
Quem causa a desaceleração do carro é o atrito entre os pneus e a estrada. Então teremos uma força de atrito se opondo ao movimento do carro, que está subindo a ladeira. Então a força aponta para o sentido oposto:
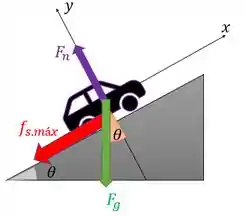
A partir desse diagrama, a gente pode usar a segunda lei de Newton e achar . Vamos assumir o sistema de coordenadas como está indicado na figura acima. A única força que não está nos eixos é a força peso, então devemos decompô-la nos eixos x e y, dessa forma:
De acordo com a 2° Lei de Newton no eixo x, temos:
As duas forças aparecem negativas no somatório porque ambas apontam para o sentido negativo de . Lembrando que :
Só que essa força de atrito é a força máxima de atrito estático, que vale
Onde é o coeficiente de atrito estático dado no enunciado. Substituindo
Falta a gente achar .
Passo 3
A 2° Lei de Newton em y, como a soma das forças em y é igual a zero, já que , pois o carro não se move em , fica:
Substituindo isso em :
Isolando :
Passo 4
Substituindo na equação de Torricelli:
E agora, substituindo pelos valores que temos:
Passo 5
Item (b)
Quando o carro está descendo a ladeira, a força de atrito estático é para cima, como mostrado no diagrama do corpo livre abaixo. Note a mudança do sistema de coordenadas, está diferente em relação ao item (a).
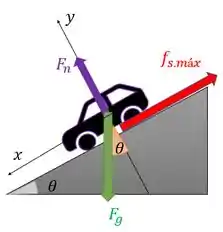
O passo a passo é o mesmo do item (a). Primeiro a gente precisa de .
De acordo com a 2° Lei de Newton no eixo x:
Aqui a componente da força peso aparece positiva porque agora ela aponta para parte positiva de .
A força de atrito continua com a mesma expressão :
E a 2° Lei de Newton em y, como ainda temos , fica:
Passo 6
Substituindo isso em :
Isolando :
A equação de Torricelli que a gente achou antes vai ser a mesma para esse caso porque temos as mesmas condições iniciais e finais:
Como a velocidade final e , então:
Substituindo :
E, por fim, substituindo por valores: