Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 60
Um bloco de está em repouso sobre um suporte de , como mostrado na figura. O suporte de está sobre uma superfície sem atrito. Os coeficientes de atrito entre o bloco de e o suporte sobre o qual ele está apoiado são e . (a) Qual é a máxima força que pode ser aplicada se o bloco de não deve deslizar no suporte? (b) Qual é a aceleração correspondente do suporte de ?
Passo 1
Precisamos montar as equações para os dois corpos separadamente, supondo que é a força máxima que pode ser feita sem que o bloco deslize,
Começamos olhando apenas para o bloco:
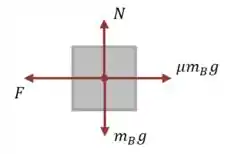
Na horizontal, temos a força puxando ele para a esquerda, e o atrito para a direita:
E analisando a vertical, descobrimos apenas que , então:
Agora vamos olhar para o suporte.
Como a polia que transmite a força é móvel, a força que ela suporta é , e o puxa para a direita:
Não temos atrito entre o suporte e a superfície, mas o atrito entre o suporte e o bloco é o mesmo de antes e puxa o suporte para a esquerda
Agora ficamos com duas equações e dias variáveis desconhecidas ( e ).
Passo 2
(a) Nosso sistema agora é:
Até aqui fizemos nossa conta pensando que o bloco não desliza, ou seja, é a aceleração do conjunto bloco-suporte.
O primeiro objetivo é calcular , mas o jeito mais fácil de fazer isso é calculando antes. Vamos somar o dobro da primeira equação com a segunda:
E agora é só substituir em qualquer uma das equações para calcular :
Passo 3
(b) Nosso próximo objetivo seria calcular a aceleração correspondente do suporte, mas vimos que, como o bloco não desliza, essa é apenas a aceleração do conjunto inteiro, que nós já calculamos:
Resposta
(a) .
(b) .