Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 80
Um avião de carga está voando horizontalmente a uma altitude de 12 km, com uma rapidez de 900 km/h, quando um grande caixote cai da rampa de acesso traseira. (Ignore a resistência do ar.) (a) Quanto tempo o caixote leva para chegar ao solo? (b) Ao atingir o solo, qual é a distância horizontal do caixote ao ponto em que ele se soltou do avião? (c) Ao atingir o solo, qual é a distância do caixote ao avião, supondo que este continuou com a mesma velocidade?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. A caixa cai do avião. Por isso, a velocidade inicial dele é a mesma do avião. E como não aceleração horizontal (porque desprezamos a resistência do ar), a velocidade horizontal dessa caixa vai ser sempre a mesma (constante).
Só que ela começa a cair, então ela está sobre ação da gravidade. Logo temos um movimento com aceleração constante na vertical e um movimento com velocidade constante na horizontal.
A figura abaixo retrata o movimento do enunciado, sendo positivo para cima:
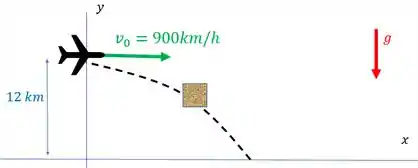
Ele quer saber o tempo que leva para essa caixa chegar no chão. Ou seja, para percorrer (negativo porque é um movimento para baixo). Já que estamos falando de uma característica vertical do movimento, podemos usar a equação da aceleração constante:
Sabemos que a componente vertical da velocidade é nula inicialmente porque só há velocidade horizontal, então . A aceleração na vertical que temos é a gravidade, dada por (ela é negativa porque está para baixo).
Substituindo esses dados e :
Isolando o tempo:
Passo 2
b) Na horizontal só temos a velocidade constante. Então podemos usar a equação de velocidade média para achar esse deslocamento horizontal que ele pediu:
é a velocidade inicial horizontal . Para passar ela para nós dividimos por :
E é o tempo decorrido até ele cair no solo, ou seja, é o tempo que achamos no item anterior. Substituindo essas duas coisas em :
Passo 3
c) Ele quer a distância entre o caixote e o avião quando o caixote está no chão.
Vamos refletir. Na horizontal a velocidade do avião é . E vimos que a velocidade do caixote é constante em também. Então enquanto ele cai, ele se move na horizontal com a velocidade igual ao do avião.
Isso faz com que ele e o avião fiquem sempre com posições iguais. Então a única distância entre eles vai ser a vertical.
A distância vertical entre o avião e o solo é , então essa é a distância entre o avião e o caixote quando ele está no solo.