Um avião voa para leste, da cidade para a cidade , em , e depois para o sul, da cidade para uma cidade , em . Para a viagem inteira, determine (a) o módulo e (b) a direção do deslocamento do avião, (c) o módulo e (d) a direção da velocidade média e (e) a velocidade escalar média.
Passo 1
Então galera, nesse tipo de exercício é sempre importante começar definindo as direções de cada eixo. Nesse caso , escolhemos um sistema de coordenadas com apontando para leste e apontando para o norte. O primeiro deslocamento é:
Enquanto que o segundo é dado como:
O deslocamento total é dado por:
Podemos achar o módulo através da relação:
Passo 2
O ângulo nós podemos achar usando a trigonometria. Sabemos que:
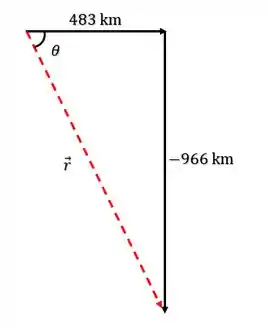
De modo que:
Sendo assim:
Isso significa ao sul do leste ou a leste do sul.
Tranquilo até aqui? Bora para o próximo item!!!!
Passo 3
Aqui nós precisamos somente jogar os valores do módulo do deslocamento e do tempo total do percurso na fórmula:
Passo 4
A direção da velocidade média sempre será a mesma do deslocamento total , ou seja , ao sul do leste ou a leste do sul.
Passo 5
Paraacharmos a velocidade escalar média só precisamos achar a distância total percorrida e jogarmos na relação:
Como temos:
Tranquilo, galera??? Bora resolver mais questões então!!!!!
Resposta
Ei, a resposta está no passo a passo :)