Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.3 - Ex. 10

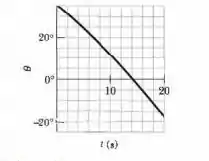
O vetor r →   =   5,00 t i →   + e t +   f t 2 j → mostra a posição de uma partícula em função do tempo t . O vetor r → está em metros, t está em segundos e os fatores e e f são constantes. A Fig. 4-31 mostra o ângulo θ da direção do movimento da partícula em função de t (   θ é medido a partir do semieixo x   positivo). Determine (a) e e (b) f , indicando as unidades correspondentes.

Passo 1

Então galera , avelocidade da partícula é dado pela derivada de   r → em relação ao tempo:

v → = d r → d t = d 5,00 t i →   + e t +   f t 2 j → d t

v → = 5,00 i → + e + 2 f t j →

O ângulo no qual se dá o movimento é, portanto :

θ = tan - 1 ⁡ v y v x = tan - 1 ⁡ e + 2 f t 5,00

O gráfico nos informa que θ 0 s = 35 ° . Sendo assim:

e + 2 f . 0 = 5,00   m / s * tan ⁡ 35 °

e = 3,5   m / s

Passo 2

O gráfico tambén nos dá que θ 14   s = 0 . Isso significa que :

e + 2 f t = 5,00 * tan ⁡ 0 °

3,5 m s + 2 f . 14   s = 0

f = - 0,125 m / s 2

Você recebeu a corrente da aprovação!!! Se quiser passar em física 1 não deixe de resolver a próxima questão e recomendar o Responde aí para 10 dos seus amigos mais próximos.

Atenção : é verdade esse bilhete rs 

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula parte da origem no instante t= 0 com uma velocidade de 8,0m s j → e se move no plano x y com uma aceleração constante igual a (4,0 i → +2 ,0j → )m / s 2 Quando a coordenada x da partícul
A posição r de uma partícula que se move no plano xy é dada por r → =2 t i →+2 sen ⁡ π 4 r a d s t j → , onde r → está em metros e tem segundos. (a) Calcule os valores das componentes x e y da posição
A posição de um elétron é dada por r=3,00 t i - 4,00 t ² j+2,00 k ² ; com t em segundos e r em metros . (a) Qual é a velocidade v ( t ) do elétron na notação de vetores unitários? Quanto vale v ( t )
Um carro se move sobre um plano x y com componentes da aceleração a x = 4m / s ²ea y = - 2 m / s ² ² ². A velocidade inicial tem componentes v o x = 8m / s e v o y = 12 m / s . Na notação de vetores u
Uma partícula se move de tal forma que a posição (em metros) em função do tempo ( em segundos) é dada por r=i+4 t ² j+t k ² Escreva expressões para (a) a velocidade e (b) a aceleração em função do tem