Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.11 - Ex. 62

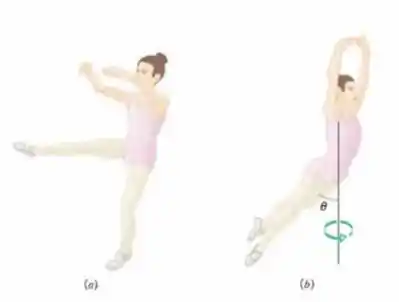
Uma bailarina começa um tour jeté (Fig. 11-19a) com uma velocidade angular ω i e um momento angular formado por duas partes: I p e r n a = 1,44   k g ∙ m 2 da perna estendida, que faz um ângulo θ = 90,0 ° com o corpo, e I t r o n c o = 0,660   k g ∙ m 2 do resto do corpo (principalmente o tronco). Quando está quase atingindo a altura máxima, as duas pernas fazem um ângulo θ = 30 ° com o corpo e a velocidade angular é ω f (Fig. 11-9b). Supondo que I t r o n c o permanece o mesmo, qual é o valor da razão ω f / ω i ?

Passo 1

Para iniciar esta questão, vamos considerar a bailarina como um corpo rígido e o eixo de rotação será fixo. Calculando o momento de inércia inicial da bailarina:

I = I p e r n a + I t r o n c o

Substituindo os valores:

I = 1,44 + 0,66

I = 2,10   k g ∙ m 2

Passo 2

Para calcular o momento de inércia final, devemos perceber que a distância horizontal do centro de massa da perna para o eixo de rotação não será mais l , será l s i n   θ . Sabendo que o momento de inércia de uma partícula pode ser calculado por:

I = m l 2

Então, o novo momento de inércia da perna é:

I ' = m l 2 sin 2 ⁡ θ

Portanto, devemos perceber que:

I ' = I p e r n a sin 2 ⁡ θ

Lembrando que agora, temos duas pernas fora do eixo de rotação, então, o momento de inércia do sistema é:

I ' ' = I t r o n c o + 2 I '

Substituindo os valores:

I ' ' = 0,66 + 2 × 1,44 × sin 2 ⁡ 30 °

I ' ' = 1,38   k g ∙ m 2

Passo 3

Sabendo que o torque resultante é nulo, então podemos aplicar a lei de conservação do momento angular:

L f = L 0

I ' ' ω f = I ω i

ω f ω i = I I ' '

Substituindo os valores:

ω f ω i = 2,10 1,38

ω f ω i = 1,52

Resposta

ω f ω i = 1,52

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola maciça homogênea rola suavemente em um piso horizontal e depois começa a subir uma rampa com uma inclinação de 15,0 ° . A bola para momentaneamente após ter rolado 1,50m ao longo da rampa. Qu
As rodas A e B na Fig. 11-61 são conectadas por uma correia que não desliza. O raio de B é 3,00 vezes maior que o de A . Qual é a razão I A / I B entre os momentos de inércia das duas rodas se elas tê
Uma menina de massa M está em pé na borda de um carrossel sem atrito de raio R e momento de inércia I que está parado. A menina joga uma pedra de massa m horizontalmente em uma direção tangente à bord
Um corpo de raio R e massa m rola suavemente com velocidade v em uma superfície horizontal e depois sobe sobe uma colina até uma altura máxima h . ( a ) Se h = 3 v 2 / 4 g , qual é o momento de inérci
Um automóvel com 1700 k g de massa acelera do repouso até 40 k m / h em 10 s . Supondo que a rodas são discos homogêneos de 32 k g determine, no final do intervalo de 10 s , ( a ) a energia cinética d