Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 63

Uma bala de 16 g é atirada contra um pêndulo balístico de 1,5 k g . Quando o pêndulo está em sua altura máxima, os fios formam um ângulo de   60 ° com a vertical. Os fios têm 2,3 m de comprimento. Determine a rapidez da bala antes do impacto.

Passo 1

Vamos dar uma olhada no que tá acontecendo aqui. A bala é atirada na direção do pêndulo, ficando dentro dele, de forma que eles sobem juntos. A gente vai ter que encontrar a velocidade que a bala estava antes de bater no pêndulo. Mas qual é a essência da questão? Colisões! E em questões de colisões o que usamos? Conservação da quantidade de movimento, coeficiente de restituição e conservação de energia. A gente só tem que achar a fórmula certa pra usar.

Passo 2

Vamos começar com a conservação da quantidade de movimento:

m v b = ( m + M ) v

v b = 1 + M m v   ( * )

Passo 3

Agora vamos usar a conservação de energia, porque temos energia cinética virando energia potencial gravitacional.

E C i n = E P o t - G r a v

M + m v 2 2 = ( M + m ) g H

v = 2 g H

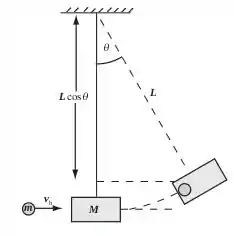
Pelo desenho, vamos concluir qual é a altura que o bloco se encontra. Do teto até o bloco com a bala, a distância vertical é de L c o s θ . Então, o bloco está a uma altura em relação ao ponto mais baixo dada por H = L - L c o s θ = L ( 1 - c o s θ ) .

v = 2 g L ( 1 - c o s θ )

Passo 4

Substituindo na equação ( * ) e trocando pelos valores:

v = ( 1 + M m ) 2 g L ( 1 - c o s θ )

v = ( 1 + 1.5 0.016 ) 2 × 9.81 × 2.3 × ( 1 - c o s 60 ° )

v = 450 m / s

Resposta

v = 450 m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 9-83, o bloco 1 desliza ao longo de um eixox em um piso sem atrito com uma velocidade de 0,75m / s até sofrer uma colisão elástica com o bloco 2, inicialmente em repouso. A tabela a seguir mos
No arranjo das duas esferas da Fig. 9-20, suponha que a esfera 1 tem uma massa de 50g e uma altura inicial h 1=9,0c m e que a esfera 2 tem uma massa de 85g . Depois que a esfera 1 é liberada e colide
Um bloco de 3,0 k g , movendo-se a 4,0 m / s , sofre uma colisão frontal elástica com um bloco estacionário de 2,0 k g . Use conservação da quantidade de movimento e o fato de que a rapidez relativa d
Uma pequena bola de borracha, de massa m , se move com rapidez v para a direita, de encontro a um taco muito mais massivo, que se desloca para a esquerda com rapidezv . Determine a velocidade da bola
Um corpo de 5,0 k g , com uma rapidez de 4,0 m / s , colide frontalmente com outro corpor, de 10,0 k g , que se move de encontro a ele com 3,0 m / s . O corpo de 10,0 k g fica parado após a colisão. (