Uma partícula de 3,0 kg, que se move ao longo do eixo x, tem uma velocidade de +2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, , que varia com a posição como mostrada na figura abaixo. (a) Qual é a energia cinética da partícula quando ela passa pela origem? (b) Qual é o trabalho realizado pela força, enquanto a partícula se move de x = 0,0 m até x = 4,0 m? (c) Qual é a rapidez da partícula quando ela está em x = 4,0 m?

Letra (b)

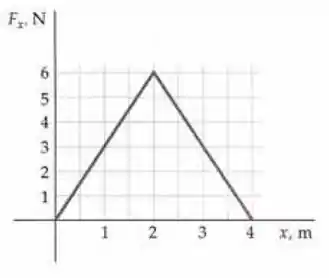
Ele quer o trabalho realizado por sobre a partícula e a gente tem o gráfico que relaciona como o deslocamento da partícula.

Lembra que o trabalho é dado pela área abaixo da curva do gráfico força versus deslocamento!

Como a força e o deslocamento são paralelos no nosso caso, o trabalho realizado por é dado pela área do nosso gráfico então. Nosso gráfico é um triângulo de base 4 e altura 6, então para achar a área podemos fazer base vezes altura sobre 2:

Letra (c)

Ele quer a rapidez da partícula em . Cara, falou de trabalho e rapidez no mesmo contexto, cê pensa logo no teorema do trabalho-energia cinética. Olha a expressão dele:

Isso diz que o trabalho total feito em uma partícula é igual à variação de energia cinética.

E lembra que temos o trabalho total realizado sobre a partícula na direção (o trabalho realizado por que calculamos no item b)

e temos também a energia cinética inicial (a energia cinética na origem que calculamos no item a)

Substituindo essas coisas:

A fórmulinha da energia cinética é:

Queremos a rapidez , então vamos isolar:

Sendo que é a energia cinética final que a gente achou no passo anterior. Aí para achar a rapidez final, vamos substituir nossos valores na expressão acima: