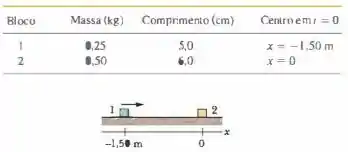
Na Fig. 9-83, o bloco 1 desliza ao longo de um eixo em um piso sem atrito com uma velocidade de até sofrer uma colisão elástica com o bloco 2, inicialmente em repouso. A tabela a seguir mostra a massa e comprimento dos blocos (homogêneos) e a posição do centro dos blocos no instante t = O. Determine a posição do centro de massa do sistema de dois blocos (a) em , (b) no instante do choque e (c) em .

Bom pessoal , no momento do choque, o centro do bloco 2 está em x = 0, a borda esquerda do bloco 2 está em e a borda da direita do bloco 1 está também em , o que significa que o centro do bloco 1 está em . Substituindo essas posições e as massas dos blocos na Eq. 9-4, obtemos [no instante

Então pessoal , poderíamos determinar as posições dos blocos no instante e usar novamente a Eq. 9-4, mas é mais fácil (e mais instrutivo) notar que na ausência de forças externas, o centro de massa do sistema se move com velocidade constante:

como pode ser verificado facilmente usando os valores para. Assim,