Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.11 - Ex. 46

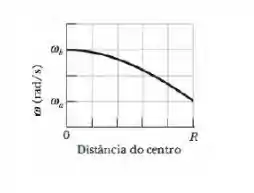
Uma barata está no centro de um disco circular que gira livremente como um carrossel, sem torques externos. A barata caminha em direção à borda do disco, cujo raio é R . A figura abaixo mostra a velocidade angular ω do sistema barata-disco durante a caminhada. A escala do eixo vertical é definida por ω a = 5 r a d / s e ω b = 6 r a d / s . Qual é a razão entre o momento de inércia do inseto e o momento de inércia do disco, ambos calculados em relação ao eixo de rotação, quando a barata chega à borda do disco?

Passo 1

Olá pessoal, tudo bem? Vamos praticar um pouco o cálculo de conservação do momento angular?

Quando a barata está no centro, ela não contribui para o momento angular do sistema, pois ela está sobre o eixo de rotação. Então na situação inicial temos apenas a contribuição do disco para o momento angular.

Quando a barata está na borda, ambos contribuem.

Passo 2

Lembrando que momento angular é L = I ω temos:

L i = L f

I d i s c o ω d i s c o = I d i s c o ω d i s c o + I b a r a t a ω b a r a t a

Na situação final ambos se movimentam com velocidade de 5   r a d / s , no início o disco se movimenta com 6   r a d / s .

Passo 3

Substituindo os valores ali em cima temos:

6 I d i s c o = 5 I d i s c o + 5 I b a r a t a

6 I d i s c o - 5 I d i s c o = 5 I b a r a t a

I d i s c o = 5 I b a r a t a

I b a r a t a I d i s c o = 1 5

Resposta

1 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O rotor de um motor elétrico tem um momento de inércia I m = 2.10 - 3 k g m ² ² em relação ao seu eixo central. O motor é usado para mudar a orientação da sonda espacial no qual está montado. O eixo d
Uma roda está girando livremente com uma velocidade angular de 800 r e v / m i n em torno de um eixo cujo momento de inércia é desprezível. Uma segunda roda, inicialmente em repouso e com momento de i
Uma barata de massa m está na borda de um disco homogêneo de massa 4 m que pode girar livremente em torno do centro como um carrossel. Inicialmente, a barata e o disco giram juntos, com uma velocidade
Uma pequena esfera maciça com 0,25 c m de raio e uma massa de 0,56 g rola sem deslizar no interior de um grande hemisfério fixo com 15 c m de raio e um eixo de simetria vertical. A esfera parte do rep
Uma pista é montada em uma grande roda que pode girar livremente, com atrito desprezível, em torno de um eixo vertical (figura abaixo). Um trem de brinquedo de massa m é colocado na pista e, com o sis