Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 14.7 - Ex. 42

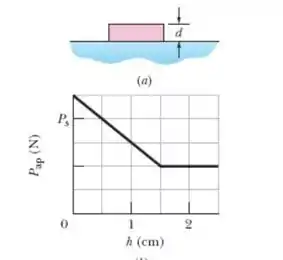
Na figura, um bloco retangular é gradualmente empurrado para dentro de um líquido. O bloco tem uma altura d ; a área das faces superior e inferior é A   =   5,67   c m ² . A Fig. 14-39b mostra o peso aparente P a p do bloco em função da profundidade h da face inferior. A escala do eixo vertical é definida por P s   =   0,20   N . Qual é a massa específica do líquido?

Passo 1

Primeiro, lembre-se que “Peso aparente” é aquele peso medido de um objeto submerso em um fluido. Tal peso é sempre menor que o peso do fluido medido fora do fluido devido à ação da força de empuxo para cima.

Esse peso é dado por P e s o a p a r e n t e = m × g - V s u b m e r s o × ρ × g .

Passo 2

Imagine um corpo totalmente submerso em um líquido, sendo mantido submerso por meio da ação de uma força externa (pode ser você segurando o objeto no fundo , por exemplo). Se esse objeto for menos denso que a água, ele tenderá a subir e, a partir do momento em que ele encontra a superfície do líquido, o seu volume submerso irá diminuir (de acordo com o que demonstra a reta descendente do gráfico) e, portanto, seu peso aparente será cada vez maior. Quando esse objeto abandona completamente o líquido, o empuxo para de atuar sobre ele e, portanto, o seu peso aparente passa a ser constante e igual a m × g (pois nesse caso V s u b m e r s o = 0 . Então, podemos perceber que a altura do bloco é igual a d = 1,5   c m , pois quando esse comprimento é atingido, o peso aparente passa a mudar de comportamento, indicando o momento em que o corpo passa a ser submerso no fluido.

Passo 3

Agora, vamos identificar o valor do “Peso real” do corpo. Certamente, ele é igual ao maior valor de peso indicado no gráfico, uma vez que o peso aparente diminui a partir do valor do peso real. Logo, temos que m × g = 0,25   N . Assim, usando a expressão anterior para calcular o empuxo quando h = 0 , temos:

V s u b m e r s o × ρ × g = m × g - P e s o a p a r e n t e = 0,25 N - 0,10 N = 0,15 N

Passo 4

Isolando ρ (densidade do fluido) na expressão acima sabendo que V = 1,5 c m × 5,67 c m 2 = 8,5 × 10 - 6   e g = 9,8   m / s ² , temos:

ρ = 0,15   N V × g ≅ 1800   k g / m ³

Resposta

1800   k g / m ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. Suponha que Arquimedes tivesse verificado que: ( i ) Colocando a coroa do rei Herão dentro de uma banheira cheio de água até a borda, 0,3l de água transbordavam; ( i i ) Era preciso aplicar uma fo
13. Um bloco cúbico de aço, de 5c m de aresta e densidade 7,8g / c m 3 , está mergulhando num recipiente com água, suspenso de uma balança de molas graduada em k g f . A massa total do recipiente e da
11. Um densímetro tem a forma indicada na figura. P . 7 , com uma haste cilíndrica graduada, ligada a um corpo que geralmente contém algum lastro. O densímetro é calibrad, mergulhando-o na água, marca
18. Um balão esférico de 5m de raio está cheio de hidrogênio. Nas condições normais, a densidade do hidrogênio é 0,0899k g / m 3 e a do ar é 1,29k g / m 3 . Desprezando o peso das paredes, qual é a fo
16. Duas bolas de mesmo raio, igual a 10c m , estão presas uma à outra por um fio curto de massa desprezível. A de cima, de cortiça, flutua sobre uma camada de óleo, de densidade 0,92g / c m 3 com a m