Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.5 - Ex. 38

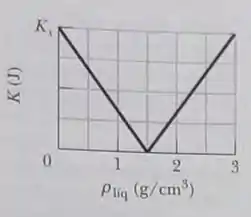
Uma pequena esfera totalmente imersa em um líquido é liberada a partir do repouso e sua energia cinética é medida depois que se desloca 4,0   c m no líquido. O gráfico mostra os resultados depois de muitos líquidos serem usados: a energia cinética   K está plotada no gráfico em função da massa específica do líquido, ρ l i q   , e a escala do eixo vertical é definida por   K s   =   1,60 J. Quais são (a) a massa específica e (b) o volume da bola?

Passo 1

  1. Lembre-se que quando um objeto possui a mesma densidade do fluido circundante ele não tenderá a boiar ou afundar no líquido, permanecendo parado. Então, o ponto correspondente a uma energia cinética nula indica o caso em que ρ l í q u i d o = ρ b o l a = 1,5   g / c m ³ .

    2. Passo 2

  2. Considere agora o caso hipotético em que ρ l í q u i d o   = 0 (ponto de energia cinética máxima). Nesse caso, a bola está efetuando um movimento imersa em um ambiente sem densidade, ou seja, o vácuo perfeito. Utilizando a conservação da energia mecânica e considerando que a bola atinge uma altura h = 4,0   c m no líquido, temos que a energia cinética antes de atingir essa altura converte-se integralmente na energia potencial:

m v 2 2 = m × g × h

Então:

v ² =   2 × g × h = 2 × 9,8 m s 2 × 0,04 m = 0,784   m ² / s ²

Utilizando o valor da energia cinética correspondente a essa situação ( K = 1,6   J - de acordo com o gráfico), temos:

K = 1,6   J = m × v 2 2 = m × 0,784     m ² / s ² 2

Isolando m , temos:

m = 4,082   k g

Passo 2

A partir dos valores de m e de ρ b o l a , podemos encontrar o volume da bola através da relação:

V b o l a = m ρ b o l a   = 4,082 k g 1,5 × 10 - 3   k g / c m 3 ≅ 2,72 × 10 3   c m 3

Resposta

a)

ρ b o l a = 1,5 g c m 3

b)

2,72 × 10 3   c m 3  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque cilíndrico com um grande diâmetro é preenchido com água até uma profundidade D = 0,30 m . um furo de seção transversal de área A = 6,5c m ² ² no fundo do tanque permite a drenagem da água. (
O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Um medidor venturi é usado para medir a velocidade de um fluido em um cano. O medidor é ligado entre dois segmentos do cano (Figura); a seção reta A na entrada e na saída do medidor é igual à seção re
Na Fig 14-38, um cubo de aresta L=0,600m e 450k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030k g / m ³ ³. Determine (a) o módulo da força total
Para descrever o tamanho de um grande navio é costume usar expressões do tipo "ele desloca 20.000 toneladas". O que isso significa? O peso do navio pode ser calculado por essa informação?