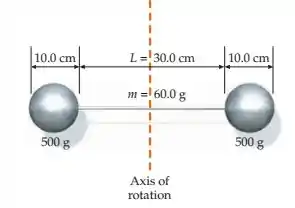
Visando participar de uma equipe de atletas, você e seu amigo Carlos resolver praticar com halteres. Cada um de vocês está usando “A Besta”, um modelo constituído de duas esferas, cada uma de e massa e de raio, presas às extremidades de uma barra uniforme de e de massa (figura 9-47). Vocês desejam determinar o momento de inércia da Besta em relação a um eixo perpendicular à barra, que passa pelo seu centro. Carlos se vale da aproximação que trata as duas esferas como partículas pontuais distantes do eixo de rotação e considera desprezível a massa da barra. Você, no entanto, resolve fazer um cálculo exato. (a) Compare os dois resultados. (Dê a diferença percentual entre eles.) (b) Suponha as esferas substituídas por duas cascas esféricas finas, cada uma com a mesma massa das anteriores, maciças. Forneça um argumento conceitual para explicar como esta substituição causa, ou não causa, uma alteração no valor de .

Enquanto isso, nós, que estudamos bastante física, vamos calcular o momento de inércia com mais rigor, considerando o sistema como uma barra e duas esferas. Só que tem uma coisa: o eixo não passa pelo centro de massa das esferas, então vamos ter que usar o teorema dos eixos paralelos (de Steiner) pra calcular.

O momento de inércia de uma barra, com relação a um eixo que passa pelo seu centro de massa é:

Para as esferas:

Logo:

Substituindo valores, vamos obter:

A diferença percentual pra estimativa do nosso amigo Carlos é de:

Ou seja, até que não fez tão mal usar a aproximação... e a gente zoando o Carlinhos...

b) A inércia da rotação iria aumentar, já que o do centro e massa de uma esfera oca é maior que o de uma esfera maciça.