Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 45
Uma roda de vagão de de diâmetro consiste em um aro fino de de massa e de raios, cada um com de massa. Determine o momento de inércia da roda de vagão em relação ao seu eixo.
Passo 1
Falaaaa, cê tá bem? Então, ele quer o momento de inércia de uma roda formada por um aro e 6 raios, em relação ao eixo de rotação, que passa pelo centro da roda.
Pra começo de conversa, uma roda com raios é algo desse estilo aqui:
Tá, isso é uma roda de um carro, e não de um vagão. Então vamos olhar pra essa figura que mostra melhor a roda do vagão mesmo
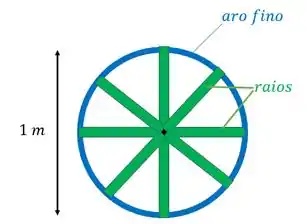
O aro é essa parte em azul e os raios são essas partes em verde, que seriam como cilindros bem finos ligando o centro da roda a borda.
E, pensa aqui, o momento de inércia de um sistema é a soma do momento de inércia dos objetos que compõem o sistema. Se esse sistema for a roda toda, a gente pode dizer que os objetos são os raios e o aro, então temos:
Então o que a gente precisa fazer é achar o momento de inércia do aro e de um raio, ambos em relação ao eixo que passa pelo centro, e depois jogar nessa expressão. Bora lá!
Passo 2
Bem, temos um aro e o eixo em relação a qual queremos o momento vai passar pelo sei centro. O momento de inércia de um aro em relação a um eixo que passa pelo seu centro é dado por
Onde é a massa do aro e é o raio do aro. Para a gente, e o raio, que é a metade do diâmetro de , vale .
Substituindo nossos dados:
Passo 3
E agora a gente precisa do momento de inércia de um raio em relação a um eixo que passa pelo sua extremidade, já que a extremidade do aro está no centro da roda.
Ele pode ser entendido como uma barra fina. A fórmula para o momento de inércia de uma barra fina em relação ao eixo passando pela sua extremidade é:
Onde é a massa de um raio, então e é o comprimento de um raio. O comprimento de um raio é exatamente o que o nome diz, o raio da roda! Então vale metade do diâmetro de , .
Substituindo os valores:
Passo 4
Já temos tudo que precisamos. A gente viu que:
Substituindo os valores:
Show de bolinhas :D