Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 44
Determine o momento de inércia de uma esfera maciça e uniforme de massa M e raio R em relação a um eixo tangente à sua superfície.
Passo 1
Falaaaa, querido! Tá bem?
Então, ele quer o momento de inércia de uma esfera maciça em relação a um eixo tangente a sua superfície. Algo assim:
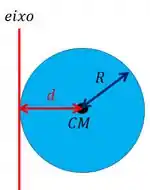
Mas se você olhar lá no livro ele só tem fórmula para o momento de inércia de uma esfera em relação a um eixo que passa pelo seu centro de massa, ou seja, em relação a um eixo que passa pelo seu centro. Ela é essa aqui
Então o que a gente faz? Desiste? Não! Vamos conseguir juntos. Bora!
Passo 2
Aqui vai ser muito útil usarmos o teorema dos eixos paralelos (ou teorema de Steiner). Por que? Porque já conhecemos o momento de inércia da esfera com relação ao seu centro de massa. O teorema tem essa cara:
Ou seja, ele relaciona o momento de inércia em um eixo paralelo ao eixo que passa pelo centro massa ao momento de inércia em relação ao eixo que passa pelo CM, a massa da esfera e , que é a distância entre esses dois eixos.
Aí esse para gente vai ser o momento de inércia em relação ao eixo que é tangente a esfera. Podemos substituir a nossa expressão para no teorema:
Poxa, mas quem é ? Cara, é a distância entre os dois eixos, o que é tangente a esfera e o que passa pelo centro da esfera. Repara pela nossa figura que essa distância vai ser exatamente o raio da esfera! Que é a distância entre o centro dela e a borda. Entao