Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 47
Uma placa retangular uniforme tem massa e lados de comprimentos e . (a) Mostre, por integração, que o momento de inércia da placa em relação a um eixo perpendicular passando por um dos vértices vale . (b) Qual é o momento de inércia em relação a um eixo perpendicular que passa pelo centro de massa da placa?
Passo 1
a) Falaaaa! Então, o enunciado quer o momento de inércia de uma placa retangular em relação a um eixo que passa por um dos seus vértices, assim:
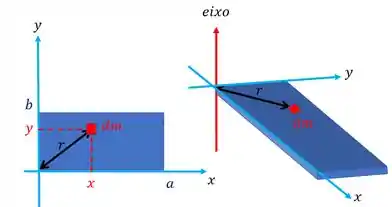
A gente não tem o momento de inércia de placas retangulares na nossa listinha do livro, né? Então vamos precisar usar integral para achar o momento de inércia.
Para fazer isso, a gente precisa montar essa integral:
Onde é a distância entre o eixo, em relação ao qual a gente quer o momento de inércia, e um elemento que pertence ao nosso sólido (a placa retangular).
Como assim “elemento”? Cara, é um pedacinho do nosso sólido. Aí esse pedacinho tem uma massa bem pequena , uma altura bem pequena e uma largura .
Bora ver como montar essa integral!
Passo 2
Percebe que é a distância da posição do nosso elemento e a origem. Essa distância pode ser calculada por Pitagoras, aí fica
E pode ser escrito também em função de e . Como? Vamos imaginar que a placa tem densidade superficial , que é dada por
Onde é a massa da placa e a área dela. Essa densidade é constante. Ela é a mesma para todos os pontos. Então a gente pode dizer que
Só que quem é é a área do elemento. Como ele tem altura e largura , a área é
Então fica:
Percebe que temos dois aí. Isso quer dizer que vamos calcular duas integrais, uma dentro da outra. Pois é, meu amigo, essa não é uma questão que vai poder ser resolvida com uma integral simples, como normalmente seria em Física 1.
Geralmente vemos essa matéria junto com Cálculo 1, só que pra mexer com duas derivadas (dois ) precisamos de coisas mais da frente. Isso pode ter te deixado embananado nela, mas vamos com calma que a gente vai sair dessa.
Passo 3
Tinhamos essa integral:
Mas ela precisa ser uma integral dupla então. Vamos colocar dois símbolos de integral ali:
Aí substituindo nossa expressão de e :
Percebe que no eixo , nossa placa está dentro do intervalo , aí esses ficam sendo os extremos de integração da integral em relação a . E no eixo , ela está em , então esses são os extremos de integração da integral em relação a .
Aí gente pode montar a integral de dentro como sendo em relação a , e a de fora como sendo em relação a . Fica assim:
É uma integral dentro da outra mesmo, a gente calcula a de dentro e depois a de fora. A gente pode tirar das duas integrais o , porque ele é constante.
Passo 4
Aí para integrar em relação a , a gente considera como um número (uma constante), aí fica assim
Agora calcula em relação a :
A gente pode escrever essa densidade superficial em função da nossa massa . Lembra que
Sendo que a massa total da placa é :
Substituindo no nosso :
Passo 5
b) Cara, agora ele quer o momento de inércia em relação ao centro de massa. Como a gente já tem o momento de inércia em relação a um outro eixo, podemos usar o teorema dos eixos paralelos (teorema de Steiner). Ele tem essa cara:
Aí é o momento que a gente achou. é o momento de inércia em relação ao centro de massa que a gente quer achar. é a massa da placa e é a distância entre o eixo que passa pelo vértice e o eixo que passa pelo centro de massa.
A gente já pode substituir nosso aí e isolar :
Passo 6
E quem é aqui? É a distância entre o vértice do retângulo e o seu centro (onde fica o centro de massa):
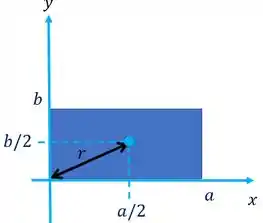
Mas olha lá no desenho: tá vendo que podemos fazer Pitágoras pra achar o ?
Como o teorema usa , a gente não precisa isolar ele. Então substituindo no teorema: