Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Exercício - Ex. 41
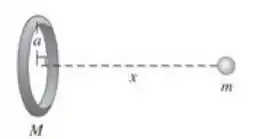
12.41. Considere o corpo em forma de anel indicado na Figura 12.35. Uma partícula de massa m é colocada a uma distancia x do centro do anel ao longo de seu eixo e perpendicularmente ao seu plano. A) Calcule a energia potencial gravitacional U desse sistema. Considere a energia potencial gravitacional igual a zero quando os dois objetos estiverem muito distantes. B) Mostre que o resultado da parte (a) se reduz ao esperado quando x for muito maior do que o raio a do anel. C) Use a relação para achar o módulo e a direção da força gravitacional exercida pelo anel sobre a partícula. D) Mostre que o resultado da parte (c) se reduz ao esperado quando x for muito maior do que a. e) Quais são os valores de U e de quando x=0? Explique por que esses resultados fazem sentido.
Passo 1
Então a gente tem a seguinte situação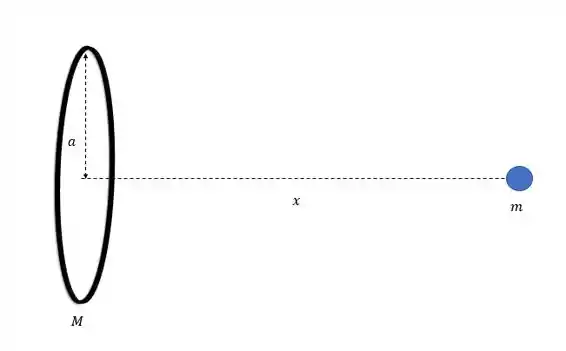
Agora imagina que a gente vai calcular a distância de c
ada segmentozinho do anel até a massa. Essa distância vai ser igual para todos os pontos do anel. Vai ser a hipotenusa de um triângulo com os catetos e
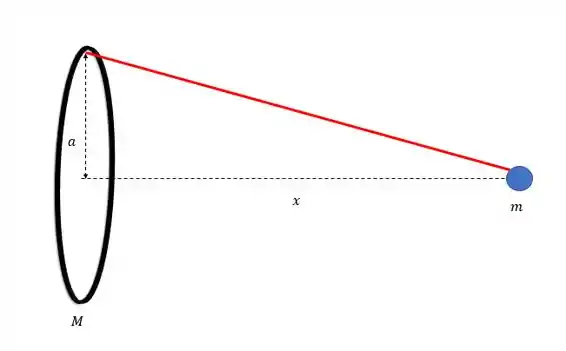
Então toda distância pode ser calculada como
E como o anel tem massa total igual a soma de todas as massas dos segmentos de anel que a gente separou, a energia potencial fica assim
Passo 2
Agora no item (b) a gente quer mostrar que se o resultado se reduz ao esperado. Mas o que é mesmo que a gente espera que aconteça? Bom o que vai acontecer é que vai se aproximar da energia potencial de uma esfera como a Terra.
Bom se então
Então fica
Que é a energia potencial de uma esfera.
Passo 3
Agora vamos para o item (c). Vamos usar a equação que o enunciado pede
Bom, a gente tem
Vamos colocar a constante para fora da derivada
Para essa derivada a gente pode usar a regra da cadeia
Então
Agora a gente faz essas derivadas mais simples
E
Então
Então
Isso vai dar
Passo 4
Agora vamos ver o que acontece se . Esse é o item (d).
O denominador se aproxima de
Então ficamos com
A gente simplifica o e temos justamente o resultado que esperamos
Passo 5
Finalmente chegamos no último item.
Vamos ver o que acontece quando .
E
Agora vamos ver por que isso acontece.
Quando a massa está exatamente no centro do anel
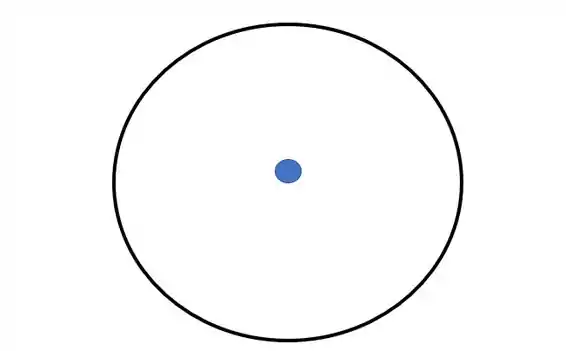
Esse é o anel visto de cima com a massa no centro. Agora imagina as forças. Cada pequeno segmento do anel vai atrair a massa para sim, então fica algo assim
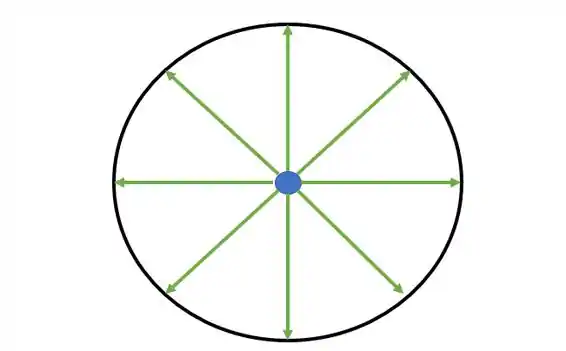
No final, todas as forças se cancelam.
Agora vamos ver a energia potencial.
Bom quando a pequena massa está no centro do anel, ela está a uma distância exata de qualquer ponto do anel. Quando você soma todas essas energias, temos
Resposta
c)
e)