Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 67

Uma barra fina não homogênea, de comprimento L , está sobre o eixo x . Uma extremidade da barra está na origem e a outra extremidade está em x = L . A massa da barra por unidade de comprimento, λ , varia como λ = C x , onde C é uma constante. (Assim, um elemento da barra possui massa d m = λ   d x .) (a) Determine a massa total da barra. (b) Determine o campo gravitacional da barra em x = x 0 , onde x 0 > L .

Passo 1

a) Vamos pegar nossa barra e separar um pedacinho bem pequeno, chamado de elemento diferencial. Ele tem comprimento d x e massa d m :

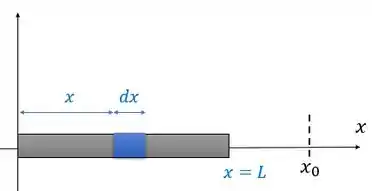
Para achar a massa de toda a barra, precisamos somar todos os d m de cada pedacinho que forma a barra, ou seja, precisamos fazer uma soma de coisinhas muito pequenas de x = 0   (começo da barra) e x = L (final da barra). Vamos usar uma integral! Podemos fazer

M = ∫ 0 L d m

O enunciado diz que d m = λ d x :

M = ∫ 0 L λ d x

Mas λ = C x !

M = ∫ 0 L C x d x

M = C ∫ 0 L x d x

Essa integral é moleza: ∫ x d x = x 2 2 . Agora é só substituir os limites de integração.

M = C x 2 2 0 L

M = C L 2 2

Passo 2

b) Cada massinha d m gera um campo gravitacional d g → , que pode ser dado por

d g → = - G d m r 2 i ^

Se a gente quer descobrir o campo em x 0 causado pela barra, precisamos achar a distância r dele até x (posição do nosso pedacinho da barra de massa d m ). Ela pode ser escrita como

r = x 0 - x

Aí o campo gravitacional causado por d m é

d g → = - G d m x - x 0 2 i ^

Lembrando que d m = λ d x

d g → = - G λ d x x - x 0 2 i ^

E que λ = C x

d g → = - G C x d x x 0 - x 2 i ^

Passo 3

Agora vamos integrar, de 0 até L , pois assim calculamos o campo gravitacional resultante causado por toda a barra (todos os pedacinhos d m da barra).

g → = - G C ∫ 0 L x d x x 0 - x 2 i ^

Precisamos resolver a integral:

I = ∫ x d x x 0 - x 2

Para isso vamos fazer uma substituição:

u = x 0 - x → x = x 0 - u

d u d x = - 1 → d u = - d x

Vamos esquecer dos extremos de integração um pouco só para resolver ela. Então a integral fica:

I = ∫ x 0 - u u 2 - d u

I = ∫ u - x 0 u 2 d u

I = ∫ u u 2 - x 0 u 2 d u

Usando propriedade de integrais para reescrever essa integral

I = ∫ 1 u d u - x 0 ∫ 1 u 2 d u

I = ln ⁡ u - x 0 - 1 u

I = ln ⁡ u + x 0 u

Lembra que u = x 0 - x :

I = ln ⁡ x 0 - x + x 0 x 0 - x

Passo 4

A gente volta então na integral original com os extremos de integração

g → = - G C ∫ 0 L x d x x 0 - x 2 i ^

g → = - G C ln ⁡ x 0 - x + x 0 x 0 - x 0 L i ^

Substituindo:

g → = - G C ln ⁡ x 0 - L + x 0 x 0 - L - ln ⁡ x 0 - x 0 x 0 i ^

Usando propriedade de log

g → = - G C ln ⁡ x 0 x 0 - L + x 0 x 0 - L - x 0 x 0 i ^

Fazendo o MMC e somando as frações

g → = - G C ln ⁡ x 0 x 0 - L - L x 0 - L i ^

Essa é a resposta. Se quiser ficar igual ao gabarito, você usa o que a gente achou no item a

M = C L 2 2 → C = 2 M L 2

Aí substituindo isso em g → , vai ficar:

g → = G 2 M L 2 ln ⁡ x 0 x 0 - L - L x 0 - L i ^

Resposta

  1. M = C L 2 2
  2. g → = 2 G M L 2 ln ⁡ x 0 x 0 - L - L x 0 - L i ^
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A esfera A , com uma massa de 80k g , está situada na origem de um sistema de coordenadas x y ; a esfera B , com uma massa de 60k g , está situada nas coordenadas ( 0,25m ,0 ) ; a esfera C , com uma m
Qual deve ser a distância entre uma partícula de 5,2 kg e uma partícula de 2,4 kg para que a atração gravitacional entre elas tenha um módulo de 2,3 × 10 - 12 N ?
Tanto o Sol quanto a Terra exercem uma força gravitacional sobre a Lua. Qual é a razão F S o l / F T e r r a entre as duas forças? (A distância media entre o Sol e a Lua é igual a distância média entr
Uma massa M é dividida em duas partes, m e M-m, que são em seguida separadas por uma certa distância. Qual é a razão m/M que maximiza o módulo da força gravitacional entre as partes?
Influência da Lua. Algumas pessoas acreditam que suas atividades são controladas pela Lua. Se a Lua estava do outro lado da Terra, ao longo de uma reta que passava por você e pelo centro da Terra, e p