Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 29
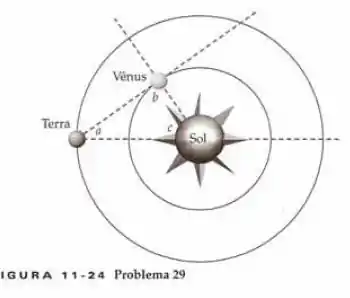
Kepler determinou distâncias no sistema solar a partir de seus dados. Por exemplo, ele encontrou a distância relativa entre o Sol e Vênus (em comparação com a distância do Sol à Terra) da seguinte maneira: como a órbita de Vênus é mais próxima do Sol do que a órbita da Terra, Vênus é uma estrela matutina ou vespertina – sua posição no céu nunca é muito distante do Sol. Considere a órbita de Vênus perfeitamente circular e a orientação relativa de Vênus, da Terra e do Sol em sua extensão máxima, isto é, com Vênus o mais afastado possível, no céu, do Sol. (a) Sob estas condições, mostre que o ângulo na figura vale . (b) Se o ângulo de elongação máxima entre Vênus e o Sol é , qual é a distância entre Vênus e o Sol em UA? (c) Use este resultado para estimar o comprimento de um ano venusiano.
Passo 1
a) Quais são as características da situação onde, visto da Terra, Vênus está mais distante do Sol? Repara que essa distância vai ser proporcional ao ângulo . Quanto maior for , maior a é a distância entre esses astros vista da Terra.
Agora imagina que você quer desenhar o máximo. Vamos deixar a Terra parada. Assim, o segmento que liga a Terra e o Sol vai permanecer onde está (já que o Sol não se mexe, né).
Então só poderemos variar o segmento que liga a Terra a Vênus.
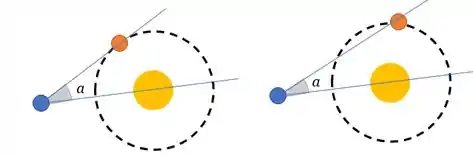
Esse segmento precisa sempre passar pela trajetória de Vênus. Percebe que para ser o maior possível, o segmento deve passar tangente a trajetória de Vênus (situação da direita). Caso contrário, o ângulo vai ser menor (situação da esquerda).
Então para Vênus parecer o mais afastado possível do Sol, visto do céu terrestre, ele vai estar passando por uma reta que sai da Terra e é tangente à sua órbita.
Como essa reta é tangente a circunferência que representa a trajetória de Vênus, o segmento que liga Vênus ao sol vai ser coincidente com o raio da circunferência. Aí o ângulo entre esse segmento e a reta tangente ao círculo vai ser .
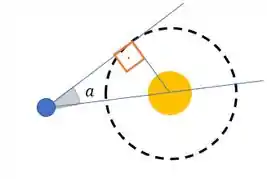
Logo, temos que .
Passo 2
b) Então, é a distância média entre a Terra e o Sol. Basicamente ele quer que a gente ache a distância entre Sol e Vênus em função da distância entre a Terra e o Sol.
Já que temos um triângulo retângulo, por trigonometria, conseguimos relacionar a distância do Sol a Vênus, usando o ângulo .
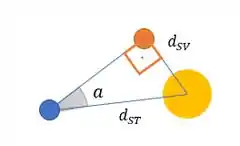
Olhando a figura podemos fazer
Temos que , então
Passo 3
c) Pra acabar, vamos usar a terceira Lei de Kepler para relacionar os períodos!
Os raios das trajetórias vão ser a distância entre o planeta e o sol. Com o valor que achamos na parte (b):