Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.6 - Ex. 48

Uma barra uniforme e fina com comprimento de 0,500 m gira em um círculo sobre uma mesa sem atrito. O eixo de rotação é perpendicular ao comprimento da barra em uma extremidade e é estacionário. A barra tem uma velocidade angular de 0,400 rad/s e um momento de inércia em torno do eixo de 3,00 103 kg m2 . Um inseto inicialmente parado sobre a barra no eixo de rotação decide pular para a outra ponta da barra. Quando o inseto atinge a ponta da barra e fica parado lá, sua velocidade tangencial é de 0,160 m/s. O inseto pode ser tratado como uma partícula. Qual é a massa (a) da barra e (b) do inseto?

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

Abaixo temos um esquema das condições iniciais e um esquema das condições finais:

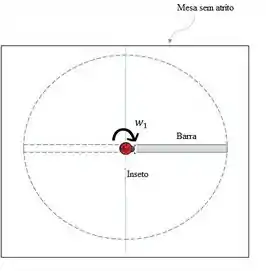
Passo 2

Letra a:

Para a massa da barra:

3.00 × 10 - 3 = 1 3 M ( 0.500 ) 2 → M = 0.036 k g

Passo 3

A velocidade angular nas condições finais é:

w 2 = v 2 L = 0.160 0.500 = 0.320 r a d s

Observe que não há forças externas produzindo torque em torno do eixo de rotação.

O peso do inseto e o peso da barra, e a força normal da mesa na barra são perpendiculares ao plano (paralelos ao eixo de rotação).

A força exercida a partir do eixo de rotação na barra é aplicada no eixo de rotação, então o braço de alavanca é zero.

Não há atrito entre a haste e a mesa.

O momento angular é conservado:

L 1 = L 2

E assim, conseguimos encontrar a massa do inseto:

I barra   w 1 + I inseto   1 w 1 = I barra   w 2 + I inseto   2 w 2

3.00 × 10 - 3 ( 0.400 ) + m ( 0 ) 2 = 3.00 × 10 - 3 ( 0.320 ) + m ( 0.500 ) 2 ( 0.320 )

m = 0.003 k g

Resposta

  1. M = 0.036 k g
  2. m = 0.003 k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma longa barra de 16,0k g , de 2,40m de extensão, está apoiada, em seu ponto do meio, sobre o fio de uma faca. Uma bola de massa de vidraceiro, de 3,20k g , cai a partir do repouso de uma altura de 1
Uma bola de 2,0k g está presa a um fio de 1,5m de comprimento e se move no sentido anti-horário (se vista de cima) em um círculo horizontal (Figura 10-56). O fio forma um ângulo θ = 30 ° com a vertica
Um corredor de 55 kg corre na periferia de uma mesa giratória montada em um eixo vertical sem atrito passando em seu centro. A velocidade do corredor em relação à Terra possui módulo de 2,8 m/s. A mes
Duas partículas de mesma massa m estão presas às extremidades de uma mola de massa desprezível, inicialmente com seu comprimento relaxado l 0 . A mola é esticada até o dobro desse comprimento e é solt
No sistema da figura, análogo a um regulador centrífugo, o anel A, de massa desprezível, pode deslizar ao longo do eixo vertical. Inicialmente, as duas bolas iguais de massa m = 200 g estão a uma dist