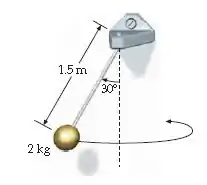
Uma bola de está presa a um fio de de comprimento e se move no sentido anti-horário (se vista de cima) em um círculo horizontal (Figura 10-56). O fio forma um ângulo com a vertical. (a) Determine as componentes horizontal e vertical da quantidade de movimento angular da bola em relação ao ponto de suspensão. (b) Determine a magnitude de e verifique que ela é igual à magnitude do torque exercido pela gravidade em relação ao ponto de suspensão.

Vamos começar achando . Ele é o vetor que sai da origem (o ponto ) e vai até a nossa bolinha. Só que repara que a bolinha está se movendo, então esse vetor não vai ter suas coordenadas constantes, mas vai depender do tempo .

Outra coisa é que se o vetor começa na origem, as componentes dele são iguais as coordenadas do seu ponto final, ou seja, basicamente vamos escrever a posição da bolinha em relação ao tempo, ok?

Vamos achar cada componente. A componente vai ser a projeção da corda em , então:

Ela é negativa porque a bolinha está em uma altura negativa em relação a origem. Agora vamos para e . Cara, percebe que em relação ao plano (visto de cima), a trajetória da bolinha é circular, porque ela fica girando em torno de ? Beleza.

Aí agora eu vou te dar um bizu, tá? Se a gente tem um movimento circular em sentido anti-horário em um plano e quer uma função de para o posição da partícula que está fazendo o movimento, usamos essa expressão:

Onde é o raio da trajetória e a velocidade angular da partícula.

O raio da tratejória para gente é a projeção da corda no plano :

Aí nossas componentes ficam

Então, por equanto, nosso vetor fica

Repara que a gente colocou na componente de , porque no nosso sistema ele é o eixo vertical, tudo bem? E os horizontais são e , por isso ficou com .

Podemos expressar o vetor posição como:

Aí para achar o vetor velocidade, vamos lembrar que

Então a gente vai derivar cada componente do nosso vetor posição e achar

Percebe que não há componenete porque ela era constante em . Aí a derivada da constante é zero.

Falta achar , né? Vamos olhar fazer um diagrama de corpo livre

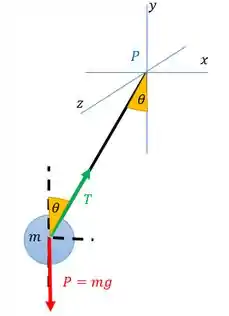
Aplicando as equações de equilíbrio

Agora repara que a componente horizontal da tensão funciona como uma força centrípeta para a partícula, então na direção dessa força (vamos chamar de direção axial), temos uma aceleração, a aceleração centrípeta. O equilíbrio fica

Mas lembra que essa aceleração tem uma expressão

Mas já vimos quando vale esse raio para o nosso movimento circular:

Então o equilíbrio fica

Relacionando as duas equações de equilíbrio que fizemos acima, temos:

Igualando essa duas expressões e isolando

Só que em é esse ? Lembra que ele veio da fórmula da aceleração centrípeta? Cara, ele é a velocidade do nosso movimento circular. Então a partir dele conseguimos a velocidade angular!

é dado por:

Portanto:

E

A quantidade de movimento angular será:

A componente horizontal, é a componente que tem e

A componente vertical, é a componente em , a que tem :

Item (b):

Vamos calcular :

Tirando o módulo, para achar a magnitude disso, temos:

Podemos colocar em evidência e tirar da raiz. Aí ficamos com a soma dos quadrados de seno e cosseno que dá um pela relação fundamental trigonométrica:

Agora temos que descobrir o valor do torque exercido pela gravidade e comparar com o valor de , para ver se o enunciado é verdadeiro.

O torque é dado por:

Isso porque o braço de alavanca do peso é a projeção da corda na horizontal. Substituindo os dados:

E é igual mesmo ao valor que achamos no passo anterior.

Ufa! Acabamos!