Uma barra de vidro. Ambas as extremidades de uma barra com índice de refração são polidas de modo a formar duas superfícies hermisféricas convexas. O raio de curvatura da extremidade esquerda é igual a e o raio de curvatura da extremidade direita é igual a . O comprimento da barra entre os vértices é igual a . O objeto para a superfície da extremidade esquerda é uma seta situada a à esquerda do vértice dessa superfície. A seta possui uma altura de e está localizada perpendicularmente ao eixo da barra. (a) Qual é o objeto para a superfície da extremidade direita da barra? (b) Qual é a distância do do objeto para essa superfície? (c) O objeto para essa superfície é real ou virtual? (Sugestão: veja o Problema 34.69) (d) Qual é a posição da imagem final? (e) A imagem final é real ou virtual? Ela é direita ou invertida em relação ao objeto original? (f) Qual é a altura da imagem final?
Passo 1
(a) O primeiro passo é fazer um desenho da situação:
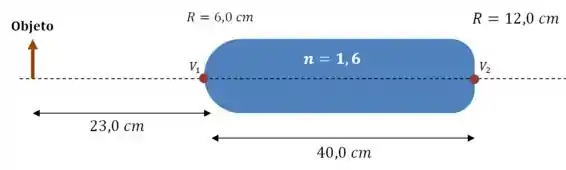
Beleza. Próxima etapa é responder o seguinte: qual é o objeto para a extremidade direita da barra?
Bom, a superfície da esquerda vai gerar uma imagem do objeto, e essa imagem vai ser o “objeto” do ponto de vista da superfície direita.
Passo 2
(b) Agora queremos calcular a distância da primeira imagem até a superfície direita.
Só lembrando: estamos falando da imagem que a superfície esquerda forma. Então beleza, vamos calcular.
Já que estamos tratando de meios com índices de refração diferentes, vamos usar essa fórmula aqui:
E todos os valores dessa fórmula já estão lá no desenho, menos a posição da imagem, que a gente quer calcular:
Ou seja, a imagem está a do vértice . Então a distância até a superfície da direita é:
Passo 3
(c) Essa imagem que está a da superfície direita vai servir como objeto para ela.
Esse objeto é real, porque está do mesmo lado dos raios que vão sair para gerar uma nova imagem depois que interagirem com a superfície direita.
Pra podermos fazer o desenho, dá até pra calcular se esse “objeto” vai ser invertido ou direito:
Como o valor é negativo, então o “objeto” é invertido:
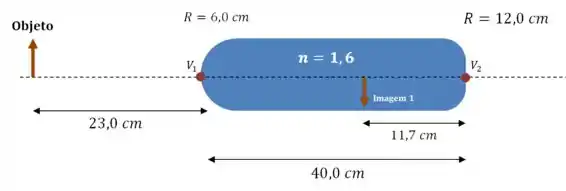
Passo 4
(d) Agora vamos calcular a posição da imagem final, que é formada quando a “Imagem 1” do nosso desenho é projetada na superfície da direita.
É só usar a mesma fórmula de antes, e os dados que estão no desenho:
O raio de curvatura é negativo porque agora o objeto está do mesmo lado do centro de curvatura da superfície (antes ele estava fora).
Vamos resolver a equação para encontrar :
Já que o sinal é negativo, então a imagem (Imagem Final) está do mesmo lado do objeto (Imagem 1):
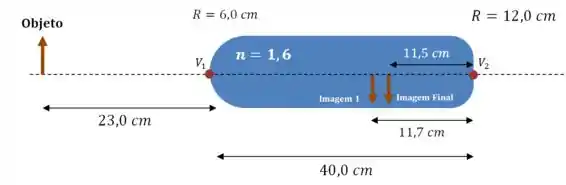
Passo 5
(e) Já que , então a imagem final é virtual.
Vamos calcular também a ampliação nesse último processo:
Como a ampliação é positiva, então a imagem final mantém a mesma orientação da Imagem 1, que era invertida.
Isso quer dizer que a imagem final é invertida em relação ao objeto original.
Passo 6
Pelo que a gente calculou até aqui, no primeiro processo a ampliação era:
E no segundo processo é:
Isso quer dizer que a ampliação total é:
E como o objeto original tinha altura , a altura da imagem final é:
O sinal negativo só diz que ela é invertida.
Resposta
(a) O objeto para a superfície da extremidade direita é a imagem produzia pela extremidade esquerda.
(b) A distância é de .
(c) O objeto é real para a superfície direita.
(d) A imagem final está à esquerda da superfície direita.
(e) A imagem final é virtual e invertida em relação ao objeto original.
(f) A imagem final tem .