Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 36

Um bastão de 30,0 cm de comprimento se move continuamente a 8,00 m/s em um plano perpendicular a um campo magnético de 500 G. A velocidade do bastão é perpendicular ao seu comprimento. Determine (a) a força magnética em um elétron no bastão, (b) o campo eletrostático no bastão e (c) a diferença de potencial entre as extremidades do bastão.

Passo 1

Fala galera! Tudo beleza?

Então, essa questão trata sobre fem do movimento. Sabemos que, quando movemos uma barra sobre um campo magnético haverá a produção de uma fem que chamamos de fem do movimento. O aparecimento dessa fem vem do fato dos elétrons livres do bastão sofrerem uma força do campo magnético, de modo a ficarem mais concentrados em uma região do bastão (veja a figura abaixo).

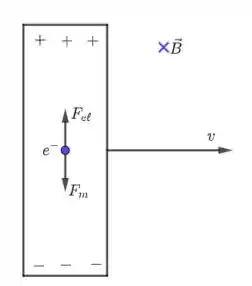
No equilíbrio, o elétron estará sujeito a duas forças: uma magnética e outra elétrica.

Passo 2

  1. O elétron terá a mesma velocidade da barra. Sendo assim, lembrando que

    2. F = q v B

    segue

    F m = 1,60 × 10 - 19 8,00 5,0 × 10 - 2 F m = 6,4 × 10 - 20   N

  2. No equilíbrio, temos que a força elétrica é igual a magnética. Sendo E o campo elétrico no interior do bastão, então a força elétrica será igual a e E .

    3. e E = 6,4 × 10 - 20 E = 6,4 × 10 - 20 1,60 × 10 - 19 = 0,40   V / m

  3. Por fim, podemos obter o valor de V lembrando da relação entre V e E :

V = E l

onde l é o comprimento do bastão. Assim,

V = 0,40 0,300 = 0,12   V

Bem, é isso galera.

Resposta

  1. 6,4 × 10 - 20   N .
  2. 0,40   V / m .
  3. 0,12   V .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está avaliando o desempenho de um eletroímã grande. O campo magnético do eletroímã é zero em t = 0 e aumenta à medida que a corrente fluindo pelos enrolamentos do eletroímã aumenta. Você determin
Na figura 30-40a, o módulo do campo magnético uniforme B → aumenta com o tempo de acordo com o gráfico da figura 30-40b, onde a escala do eixo vertical é definida por B s = 9,0m T e a escala do eixo h
Para a situação mostrada na Fig. , a = 12c m , b = 16 c m . A corrente no fio longo e reto é dada por i = 4,5A / s 2 r 2 - ( 10A / s ) t. Ache a fem na espira quadrada em t = 3,0s .
Em torno de um núcleo cilíndrico de área de seção transversal 12,2c m 2 são enroladas 125 voltas de fio de cobre isolado. Os dois terminais sāo conectados a um resistor. A resistência total do circuit
N a Fig., seja o fluxo na espira Φ u ( 0 ) no instante t = 0 . Entäo o campo magnético B → varia de maneira contínua, mas de uma forma não-especifica, em intensidade e sentido, entăo, no instante t o