Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 30.4 - Ex. 14
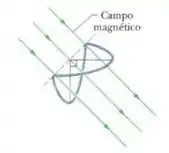
A figura 30-47 mostra uma espira formada por um ar de semicircunferencias de de raio situadas em planos mutuamente perpendiculares. A espira foi formada dobranco uma espira plana ao longo de um diâmetro até que as duas partes ficassem perpendiculares. Um campo magnético uniforme de módulo é aplicado perpendicularmente ao diâmetro de dobra, fazendo ângulos iguais (de ) com os planos das semicircunferências. O campo magnético é reduzido para zero a uma taxa uniforme durante um intervalo de tempo de . Determine (a) o valor absoluto e (b) o sentido (horário ou anti-horário, do ponto de vista do sentido de incidência de e da força eletromotriz induzida na espira durante esse intervalo.
Passo 1
Fala aí! tudo certinho?
Bom, galera, um cara chamado Faraday descobriu que uma força eletrmotriz e uma corrente podem ser induzidas em uma espira fazeno variar a quantidade de campo magnético que atravessa a espira. Ele ainda percebeu que a dita “quantidade de campo magnético” pode ser visualizada em termos das linhas de campo magnético que atravessam a espira.
O número de linhas que atravessam a espira não importa; os valores da força eletromotriz e da corrente induzida são determinados pela taxa de variação desse n��mero. O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
A primeira coisa que vamos fazer aqui é saber como fica o campo magnético nessa situação. Sabemos que a fórmual pro fluxo magnético é . Assim, aplicando as informações dadas no enunciado, temos:
Veja só!
Passo 2
Agora, tendo em mãos o fluxo magnético na espira, podemos calcular a força eletromotriz induzida!
Substituindo os valores do enunciado, temos
O sentido da fem induzida é o sentido horário, do ponto de vista do sentido de incidência de .
E aí! entendeu tudo? Responde Aí!
Resposta
- ;
- O sentido da fem induzida é o sentido horário, do ponto de vista do sentido de incidência de .