Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 13

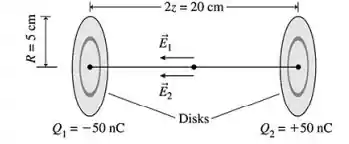
Dois discos com 10 cm de diâmetro são colocados frente a frente e afastados por 20 cm. O disco da esquerda é carregado com - 50   n C , e o da direita, com   + 50   n C .

  1. Qual é o campo elétrico E → , em módulo e orientação, no ponto eqüidistante aos dois discos?
  2. Qual é a força F →   exercida sobre uma carga de - 1,0   n C colocada no ponto equidistante?

Passo 1

Faaaaaala, galera... Tranquileba??

Fazendo um desenho do que o enunciado passa nós temos:

Precisamos definir o campo elétrico do disco a um ponto com uma distancia z do disco. Assim:

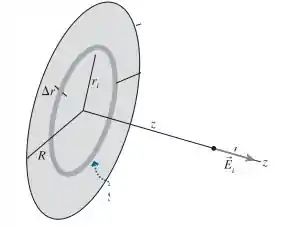
Sabemos pela definição de campo que:

E i = 1 4 π ε 0 ∫ d q r ' 2

Vemos que o campo em x e y se cancelam, logo:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ d q r ' 2 cos ⁡ θ

Sabemos que a densidade de carga é dada por:

η = q A

d q = η   d A = η d π r 2 = η 2 π r   d r

Assim:

E → =   1 4 π ε 0 ∫ η 2 π r d r r ' 2 cos ⁡ θ

Para:

r ' = r 2 + z 2 1 2

E:

cos ⁡ θ = r r ' = r r 2 + z 2 1 2

Assim ficando:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ η   2 π r d r r 2 + z 2   r r 2 + z 2 1 2 = η z 2   ε 0 ∫ r r 2 + z 2 3 2   d

Integrando de 0 ≤ r ≤ R , temos que o campo sobre um disco é:

E → = η 2 ε 0 1 - z R 2 + z 2

Para z ≫ R :

E → = η 2 ε 0 1 - 1 R 2 z 2 + 1

Este é o campo elétrico para quaisquer dos dois discos.

Passo 2

Sabemos que a densidade de carga na superfície do disco é

η = Q A

η = Q π r 2 = 50 × 10 - 9 C π 0.0 . 5   m 2 = 6.366 × 10 - 6   C m 2

Assim, como pedido o campo para z = 0.1   m para o campo E 1 →

E 1 → = 6.366 × 10 - 6   C m 2 2 8.85 × × 10 - 12 C 2 N m 2 1 - 1 ( 0.05   m ) 2 ( 0.1   m ) 2 + 1 = - 3 . 8 × 10 4 N C

Logo vemos que:

E 1 → = 3 . 8 × 10 4 N C

Para a esquerda

Vemos que o desenho nos mostra que os campos apontam para o mesmo lado, e sendo equidistante e de mesmo modulo, logo   E 1 → = E 2 →

E → = E 1 → + E 2 → = 7.6 ×   10 4   N C

Para a esquerda.

Passo 3

Sabendo que:

F → = q E →

Assim, para q = - 1.0 × 10 - 9   C , como pedido:

F → = - 1.0 × 10 - 9   C 7.6 × 10 4   N C = - 7.6 × 10 - 5 N

Para a esquerda. Ou simplesmente F → = 7 . 6 × 10 - 5 N para a direita.

Resposta

Para a)

E → = 7.6 × 10 4 N C

Para a esquerda.

Para b)

F → = 7.6 × 10 4 N C

Para a direita.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco não condutor de raio a está no plano z = 0 com seu centro na origem. O disco está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em em (a) z = 0,2 a , (b) z = 0,5 a
Usando uma planilha eletrônica ou uma calculadora gráfica faça um gráfico da intensidade do campo elétrico no eixo de um disco que tem um raio a = 3,00c m e uma densidade superficial de carga σ = 0,50
Um bastão plástico não condutor, fino e longo, é dobrado para formar uma circunferência de raio a . Entre as extremidades do bastão permanece um pequeno espaçamento de comprimento l , onde l ≪ a . Uma
Um anel uniformemente carregado tem um raio a , está um plano horizontal e tem carga negativa - Q . Uma pequena partícula está localizada no eixo do anel. (a) Qual é o mínimo valor de q / m tal que a
Um anel estacionário de raio a está no plano y z e tem uma carga positiva uniforme Q . Uma pequena partícula com massa m e carga negativa - q está localizada no centro do anel. (a) Mostre que se x ≪ a