Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 62

62. Um bloco de 200   g , preso a uma mola horizontal, oscila com amplitude de 2,0   c m e freqüência de 2,0   H z . Exatamente quando ele está passando pelo ponto de equilíbrio, movendo-se para a direita, um golpe seco direcionado à esquerda exerce uma força de 20   N sobre o bloco por 1,0   m s . Quais são as novas (a) freqüência e (b) amplitude?

Passo 1

Opa! E aí brother! Aqui vamos nós de novo!

a) Se liga só! Pra essa primeira letra, temos que indicar a nova frequência do bloco, quando lhe é aplicada uma golpe tal.

Bom! A resposta é simples : " a   m e s m a " .

A frequência de um objeto em movimento harmônico simples é independente da amplitude e ou da velocidade máxima. Logo a nova frequência é igual à frequência antiga de 2,0   H z . Molezinha, né não!?

Passo 2

b) Agora complicou um pouco! Porque a amplitude! Essa sim vai variar!

Focando no M H S do bloco quando nenhuma ação externa enxerida atua no bloco, temos o exposto na imagem abaixo...

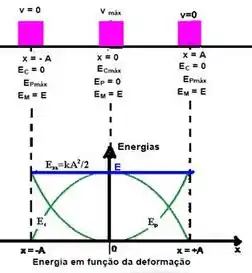
Desse modo, igualando as energias da mola na posição de equilíbrio e quando ela está na distensão máxima, temos que...

1 2 k A 2 = 1 2 m v m á x 2

k A 2 = m v m á x 2

Isolando o v m á x e substituindo os valores de cada variável;

v m á x = k A 2 m

v m á x = A ⋅ k m

Bom! Sabemos que k / m é nada mais nada menos do que a frequência angular ω do nosso sistema. Sendo assim;

v m á x = ω A

E como ω = 2 π f ...

v m á x = 2 π f A

v m á x = 2 π ( 2,0   H z ) ( 0,02   m )

v m á x = 0,25   m / s

Passo 3

Estamos indo bem!

Agora presta atenção! A questão nos informa a força imprimida sobre o bloco e o tempo em que essa força está sendo exercida. Isso só pode significar uma coisa?

É isso mesmo, meu brother! Vamos ter que usar o teorema impulso – quantidade de movimento pra resolver essa questão.

Conhecemos o valor da velocidade antes da aplicação da força. Desse modo, a velocidade depois da aplicação da força, que chamaremos de v f pode ser dada usando a relação abaixo... Lembrando que como a força é aplicada na direção contrária ao movimento inicial do bloco, seu sinal é negativo:

F ⋅ ∆ t = m v f - m v 0

- 20   N ⋅ 0,001   s = 0,2   k g v f - 0,2   k g ⋅ ( 0,25   m / s )

0,2   k g v f = ( 0,3   k g ⋅ m / s )

v f = 0,3   k g ⋅ m / s 0,2   k g

v f = 0,15   m / s

Essa é a velocidade final após a aplicação da força.

E finalmente, como sabemos que a velocidade é o produto da amplitude pela frequência angular, que se mantém constante. Então, a nova amplitude A n o v a vale...

v f = ω A n o v a

v f = 2 π f A n o v a

0,15   m / s = A n o v a ( 2 π ⋅ 2,0   r a d / s )

A n o v a = 0,15   m / s 2 π ⋅ 2,0   r a d / s

A n o v a = 0,0119   m = 1,19   c m

Pronto! Terminamos por aqui!

Até a próxima!

Resposta

a) 2,0   H z

b) A n o v a = 0,0119   m = 1,19   c m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59. Uma argola circular de massa M e raioR é pendurada a um eixo, conforme mostra a FIGURA P 14.59 . Obtenha uma expressão para a freqüência de pequenas oscilações.
61. Um deslizador de 500g , com uma mola de constante elástica de 10N / m preso a ele, encontra-se em repouso sobre um trilho de ar praticamente desprovido de atrito. A partir de uma extremidade afast
64. A FIGURA P14.64 é uma vista superior de um objeto de massa m preso entre duas tiras de borracha, esticadas, de comprimento L . O objeto encontra-se em repouso sobre uma superfície desprovida de at
66. Um cubo de gelo pode deslizar em torno do interior de um aro circular de raio R . Ele efetuará oscilações de pequena amplitude se for deslocado da posição de equilíbrio, no ponto mais baixo do aro