Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 59
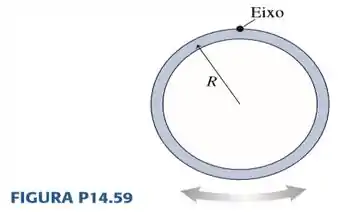
59. Uma argola circular de massa e raio é pendurada a um eixo, conforme mostra a FIGURA . Obtenha uma expressão para a freqüência de pequenas oscilações.
Passo 1
Se liga só! Primeiramente, vamos fazer uma imagem pra representar melhor o que está acontecendo em nosso problema.
E aqui está...
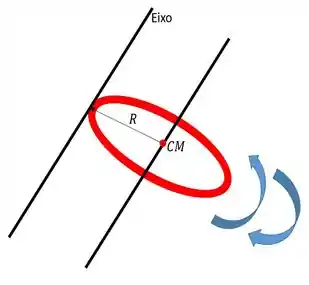
Bom! Nós sabemos que o momento de inércia em relação ao centro de passa desse disco é dado por...
Acontece que o eixo de rotação desse disco está a uma distância do eixo do centro de massa. Sendo assim, o momento de inércia total desse nosso disco em relação ao eixo em que ele está girando vale...
Passo 2
Peguemos então, a fórmula da frequência para pequenas oscilações...
A variável é nada mais nada menos do que a distância do eixo de rotação até o eixo onde passa o centro de massa, ou seja .
Desse modo, ficamos com...
Essa é a nosso expressão para a frequência, que procurávamos...