Exercícios de Posição e Fase do MHS - Lista de Exercícios Resolvida
Questão 1
Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA:
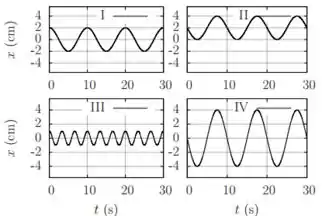
- Todos, exceto oscilam com período de
- e partem de sua posição de equilíbrio em
- e oscilam com a mesma amplitude.
- oscila com frequência menor que todos os restantes.
- realiza oscilações por minuto.
Questão 2
Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).
- Encontre a amplitude do movimento da sombra projetada no solo.
- Encontre o período e a frequência angular deste movimento.
- Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
- Faça um gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.
Questão 3
Qual é a constante da fase do oscilador harmônico cuja função aceleração aparece na Fig. 15-56 se a função posição é da forma e ?
Questão 4
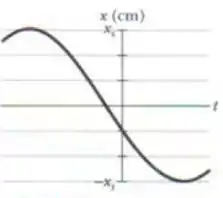
Qual é a constante de fase do oscilador harmônico cuja função posição aparece na figura abaixo, se a função posição é da forma ? A escala do eixo vertical é definida por = 6,0 cm.
Questão 5
A figura abaixo mostra um gráfico de posição tempo de um oscilador harmônico simples:
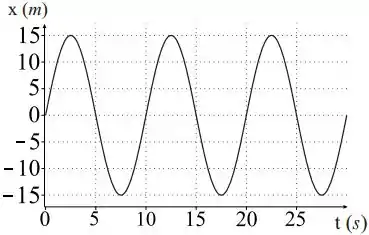
A função que melhor descreve o movimento do oscilador harmônico mostrado no gráfico acima é dada por:
Questão 6
A figura abaixo mostra a posição de um bloco oscilando em MHS na extremidade de uma mola . Quais são
a) a velocidade e b) o módulo da aceleração radial de uma partícula circular uniforme correspondente?
Questão 7
A figura de Lissajous abaixo descreve o movimento de uma massa sujeita a duas forças restauradoras perpendiculares, independentes, e . Qual é a razão entre as constantes destas forças restauradoras?
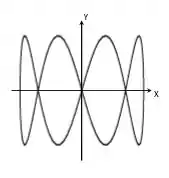
2
Ver solução completa
Questão 8
A figura abaixo mostra um gráfico de posição tempo de um oscilador harmônico simples.
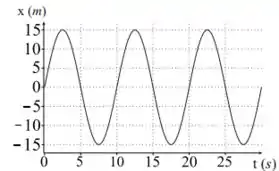
A função que melhor descreve o movimento do oscilador harmônico mostrado no gráfico acima é dada por:
Questão 9
Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA:
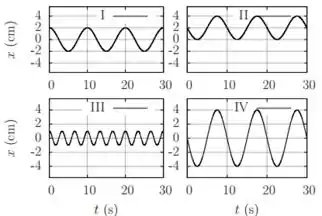
- Todos, exceto oscilam com período de
- e partem de sua posição de equilíbrio em
- e oscilam com a mesma amplitude.
- oscila com frequência menor que todos os restantes,
- realiza oscilações por minuto.
Questão 10
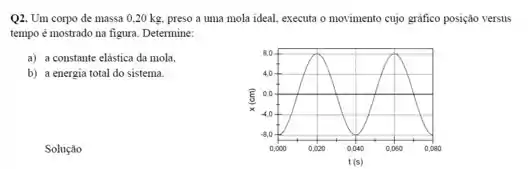
O gráfico mostra a oscilação de um bloco de massa preso a uma mola. Responder justificando:
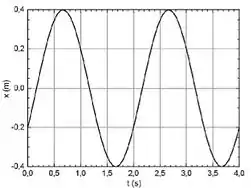
- Qual é a constante elástica da mola?
- Qual é o módulo da velocidade do bloco ao passar pela posição de equilíbrio?
- Qual é a constante de fase?
Questão 11
Num museu, um quadro circular de um pintor modernista é pendurado por um ponto da borda, como mostra a figura. Um visitante inadvertidamente esbarra no quadro, que passa a executar pequenas oscilações em torno do ponto .
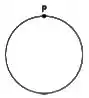
Sabendo que o raio do quadro é e que seu momento de inércia em relação a um eixo perpendicular passando pelo centro de massa é , onde é sua massa, a frequência angular das pequenas oscilações do quadro é:
- Não é possível determinar sem saber a massa do quadro.
Questão 12
O gráfico a seguir mostra como a posição de um móvel oscila com o tempo . A lei horária da posição deste objeto é melhor descrita por
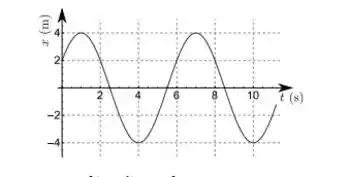
- (
Questão 14
. Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA.
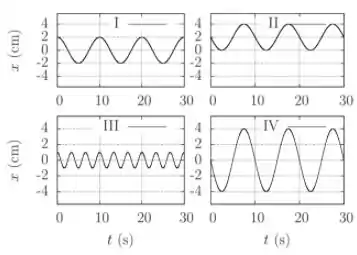
oscila com frequência menor que todos os restantes.
e partem de sua posição de equilíbrio em .
e oscilam com a mesma amplitude.
e oscilam com período de .
realiza oscilações por minuto.
Ver solução completaQuestão 15
A figura mostra as curvas obtidas em três experimentos diferentes para o deslocamento horizontal em relação à posição de equilíbrio, , de um mesmo sistema bloco-mola que oscila descrevendo um movimento harmônico simples. Qual alternativa é correta?
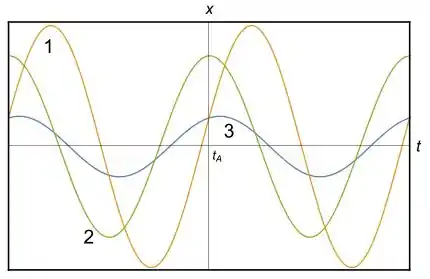
(a) Em , o módulo da aceleração do bloco no experimento 2 é menor que no experimento 1 e maior que no experimento 3.
(b) Em , a energia potencial elástica no experimento 1 é maior que a energia potencial elástica nos experimentos 2 e 3, sendo a energia potencial elástica no experimento 3 menor que no experimento 2.
(c) Em , o módulo da velocidade do bloco no experimento 1 é maior que nos experimentos 2 e 3.
(d) A freqüência angular do sistema nos três experimentos é diferente.
(e) Em , a energia cinética do bloco no experimento 2 é maior que no experimento 3.
Ver solução completaQuestão 16
Duas partículas executam movimentos harmônicos simples de mesma amplitude (A) e mesmo período (T) ao longo de retas paralelas muito próximas. Existe uma diferença de fase de entre os movimentos. Considere que a partícula 2 está atrasada em relação à primeira e que a posição da primeira é descrita por
a) Escreva a posição da segunda partícula, .
Faça (no caderno de respostas) o gráfico das posições e das partículas em função do tempo para o intervalo (indique, os zeros e os pontos de máximo e mínimo das
funções).
b) Determine a distância entre as partículas (em termos de A) quando a partícula mais atrasada passar pelo ponto de maior deslocamento.
c) Determine, em função de A, em que posições as partículas passam uma pela outra.
d) Determine, em função de A e T, as velocidades das partículas nessas posições do item (c).
Ver solução completaQuestão 17
Um movimento harmônico simples de um objeto é descrito pelo gráfico mostrado na figura abaixo. Qual é a equação da posição do objeto em função do tempo ?
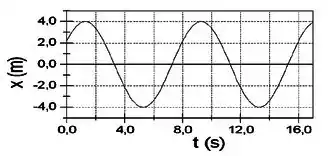
Questão 18
Um oscilador harmônico simples é formado por um bloco preso a uma mola com . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de . A figura ao lado representa o gráfico da velocidade do bloco em função do tempo t. Considere . Cuidado com os sinais!
Dados:
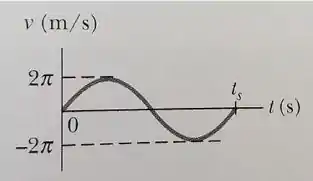
a) Qual é o período do MHS?
b) Qual é a massa do bloco?
c) Qual o deslocamento do bloco no instante ?
d) Qual é a aceleração do bloco no instante ?
Ver solução completaQuestão 19
Um corpo de massa está em movimento harmônico sobre uma superfície horizontal sem atrito e preso a uma mola ideal. O gráfico mostra a posição do corpo em função do tempo . Qual é a energia cinética máxima do corpo?
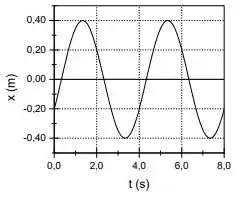
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 20
A figura ao lado mostra o gráfico da posição em função do tempo de um oscilador harmônico simples, constituído de um sistema massa-mola com constante elástica . Determine:
- a velocidade inicial da massa em
- o valor máximo de sua energia cinética em joules.
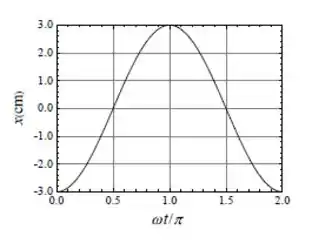
Questão 21
A posição de uma partícula é dada por , onde é dado em segundos. Seja o primeiro instante após em que a partícula passa pela origem e seja sua velocidade neste instante. Podemos afirmar que:
Questão 22
Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).
- Encontre a amplitude do movimento da sombra projetada no solo.
- Encontre o período e a frequência angular deste movimento.
- Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
- Faça uma gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.
Questão 24
Um oscilador harmônico fracamente amortecido é descrito pela equação e a posição da massa em função do tempo é mostrada no gráfico abaixo. Para uma massa , os valores de e mais apropriados para este oscilador (dica: são:
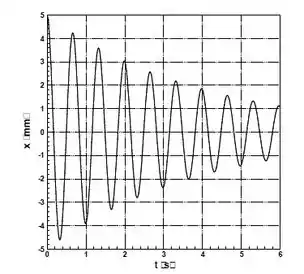
Questão 25
Um tubo de secção transversal é dobrado na forma de um . Um fluído é inserido no tubo ocupando um comprimento do tubo. O fluido é sugado de um lado do tubo e então é solto, resultando em um movimento oscilatório (considere que não tem atrito).
Mostre que o período de oscilação do movimento harmônico resultante é dado por:
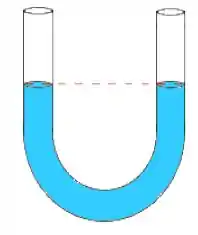
Questão 27
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
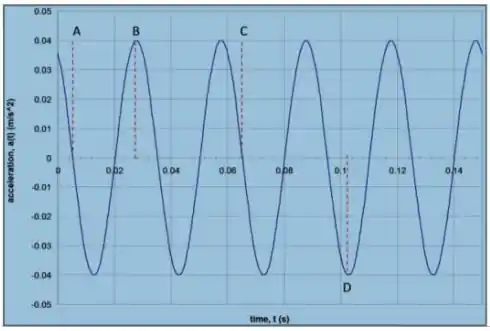
O deslocamento máximo do corpo.
Ver solução completaQuestão 28
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
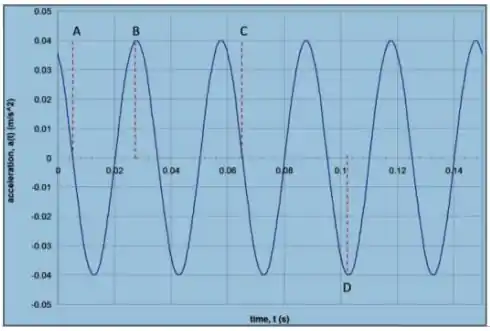
A constante de fase do movimento.
Ver solução completaQuestão 29
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
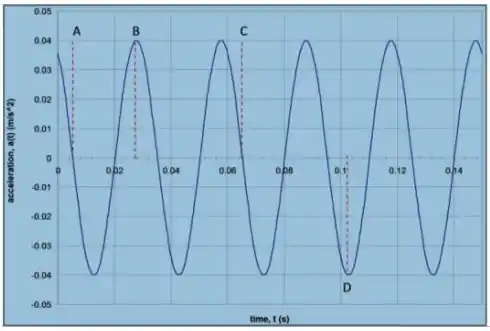
A constante elástica da mola.
Ver solução completaQuestão 30
O gráfico ao lado mostra a variação de aceleração de um corpo de oscilando horizontalmente preso à uma mola. Observando a figura determine:
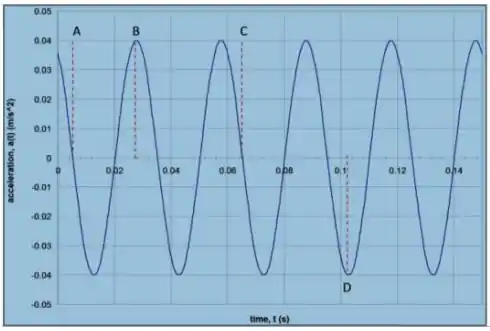
A constante elástica da mola.
Ver solução completaQuestão 31
O movimento harmônico simples de um objeto é descrito pelo gráfico mostrado abaixo. Como se escreve a equação da posição deste objeto em função do tempo, onde x(t) é expresso em m e t em s?
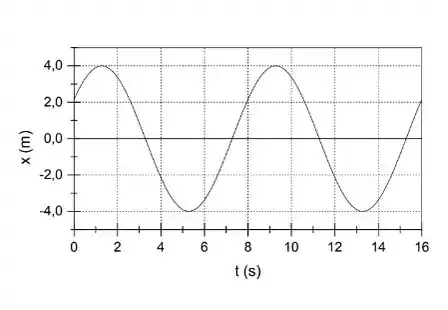
a)
b)
c)
d)
e)
Ver solução completaQuestão 32
Os três gráficos da figura ao lado representam a posição em função do tempo, , de partículas realizando diferentes movimentos harmônicos simples, identificados pelas letras H, K e J. Se as velocidades máximas das partículas são dadas por , e para os movimentos H, K e J, respectivamente, e , e são as respectivas frequências angulares dos movimentos, podemos afirmar que:
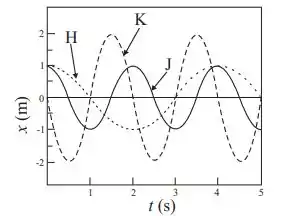
a) e .
b) e .
c) e .
d) e .
e) e .
Ver solução completaQuestão 33
Qual dos seguintes gráficos representa um movimento harmônico simples com amplitude e frequência angular ?
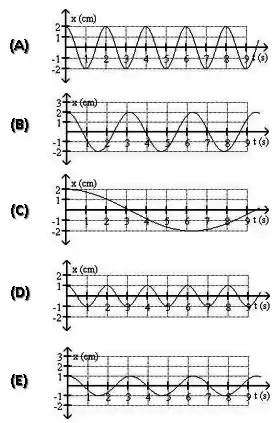
Questão 34
Uma partícula de massa oscila harmonicamente com equação .
- Qual a frequência e o período desta oscilação?
- Faça os gráficos da posição e da velocidade entre os instantes e , indique corretamente no gráfico os valores da posição e da velocidade no gráfico correspondente para . Indique também no eixo vertical os valores máximos e mínimos para
- Faça os gráficos da energia cinética e da energia mecânica total entre os instantes e . Indique corretamente no gráfico os valores da energia cinética e da energia mecânica correspondente para . Indique também no eixo vertical os valores máximos de e .
Questão 35
O gráfico abaixo mostra a oscilação horizontal de um bloco de massa 0,20 kg preso a uma mola ideal.
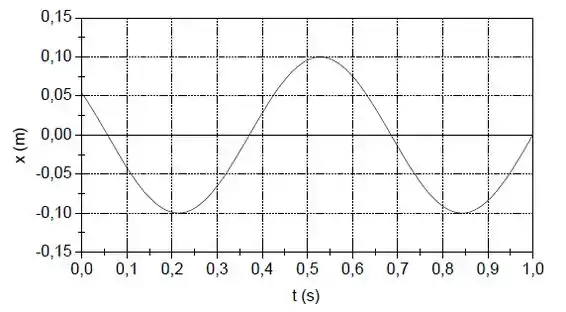
a) Qual a constante elástica da mola?
b) Escreva a equação que descreve x(t).
c) Qual é o módulo da velocidade do bloco ao passar pela posição de equilíbrio?
Ver solução completaQuestão 36
Um ponto move-se sobre a circunferência de raio desacelerando, de modo que no cada instante os módulos da aceleração radial e transversal são iguais. Sabendo que no instante a velocidade angular do ponto é igual a . Encontre, usando coordenadas polares:
- A velocidade angular do ponto.
- A velocidade do ponto.
- A aceleração do ponto.
Formulário:
Ver solução completaQuestão 37
O gráfico mostra a velocidade em função do tempo de uma partícula de massa , ligada a uma mola, que move-se em movimento retilíneo sobre uma mesa horizontal sem atrito, realizando um MHS. A velocidade inicial da partícula é . A expressão do deslocamento da partícula em função do tempo é:
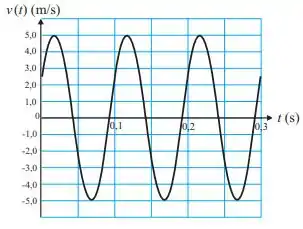
a)
b)
c)
d)
e)
Ver solução completaQuestão 38
Considere a representação gráfica de um movimento harmônico simples de uma partícula, mostrada na figura. Quando a partícula está no ponto A do gráfico, o que se pode dizer a respeito da posição e da velocidade da partícula?
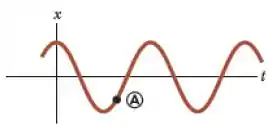
a) a posição é negativa e a velocidade é positiva;
b) a posição é positiva e a velocidade é negativa;
c) a posição e a velocidade são ambas negativas;
d) a posição e a velocidade são ambas positivas;
e) a posição é positiva e a velocidade é zero;
Ver solução completa