Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 66
66. Um cubo de gelo pode deslizar em torno do interior de um aro circular de raio . Ele efetuará oscilações de pequena amplitude se for deslocado da posição de equilíbrio, no ponto mais baixo do aro. Obtenha uma expressão para o período dessas oscilações de pequena amplitude.
Passo 1
Opa! E aí brother! Aqui vamos nós de novo!
Se liga só! A primeira coisa que devemos fazer, é um esboço pra representar melhor o que está acontecendo, inclusive posicionando um referencial pra entendermos o problema do jeito mais claro possível.
E aqui está nossa bela figura...
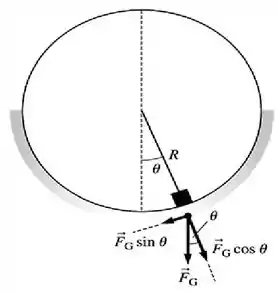
Conforme podemos ver, existem duas direções aí nesse figura para analisarmos, a direção radial e a direção tangencial.
Ah! Tem outro pequeno detalhe também que é importantíssimo! Precisamos assumir que o tamanho do cubo de gelo seja muito menor que e que é um pequeno ângulo.
Só assim, nosso cubo poderá fazer suas oscilações!
Passo 2
Aí já sabe o que tem que fazer, né companheiro!?
A força gravitacional é a responsável por influenciar no movimento do nosso cubo!
Desse modo, partiu usar a lei de Newton. Façamos o somatório das forças na direção tangencial... Lembrando que como a força tangencial faz a corpo girar no sentido horário; uma vez que por convenção adota-se geralmente o sentido anti-horário como positivo, a componente da nossa força peso ficará negativa
Como a aceleração angular é o mesmo que...
Logo, obtemos que...
Lembra lá do movimento pendular qual é a fórmula da frequência angular. Pois bem! Se não lembra, aqui está ela...
No caso pro nosso problema, o raio é o nosso ...
Acontece que a nossa fórmula obtida anteriormente foi...
Tem um nesssa fórmula. Que é justamente o quadrado da frequência angular . Sendo assim, ficamos com;
Como estamos trabalhando com ângulos muito pequenos, então...
E obtemos assim, que...
Passo 3
Finalmente, para obter o período de oscilação basta usar a fórmula abaixo...
Uma vez que...
Então;
E pronto! Terminamos aqui!
Até a próxima!