Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 64
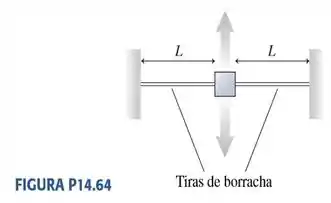
64. A FIGURA P14.64 é uma vista superior de um objeto de massa preso entre duas tiras de borracha, esticadas, de comprimento . O objeto encontra-se em repouso sobre uma superfície desprovida de atrito. No equilíbrio, a tensão em cada tira de borracha é . Encontre uma expressão para a freqüência das oscilações perpendiculares às tiras de borracha. Suponha que a amplitude seja pequena o suficiente para que o módulo da tensão nas tiras permaneça essencialmente inalterado enquanto a massa oscila.
Passo 1
Opa! E aí brother! Lá vamos nós de novo!
Se liga só! A primeira coisa que devemos fazer, é um esboço pra representar melhor o que está acontecendo melhor nesse nosso problema!
E aqui está...
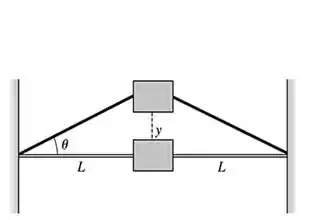
Como nosso objeto executa um , então é preciso assumir que o valor do ângulo é bem pequeno.
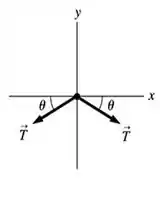
Quanto as forças que obviamente atuam em nosso bloco, temos o seguinte diagrama de corpo livre para o nosso objeto, com duas forças de tração presentes.
Passo 2
Terminada esse parte introdutória, chatinha, bora pro que interessa!
Apliquemos o somatórios das forças na direção , usando a lei de Newton;
E depois, vamos focar na primeira figura do ...
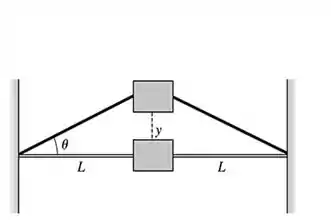
Bom! Por essa figura, tá bem claro que...
Passo 3
Na nossa oscilaçao, quando o valor de é muito pequeno, de maneira que , pegando a relação anterior, nós podemos aproximá-la de tal forma que;
Só que pela figura é na verdade, a tangente de . Logo, temos que...
Isto é claro, para ângulo muito pequenos e muito menores que radiano.
Passo 4
Voltando à lei de Newton...
Com as novas relações que obtivemos, chegamos à...
Só que...
O que nos leva, então, à...
Esse é tipo uma constante, que nem a constante do sistema massa-mola. Pra falar a verdade, esses dois sistemas são bem parecidos.
Que tal dar um nome essa constante!? Chamemos ela de ...
Passo 5
Finalmente, para obter a frequência de oscilação, basta usar a fórmula abaixo para oscilação... Como nosso sistema é bem parecido com o sistema massa-mola, usemos a mesma fórmula abaixo da frequência do sistema massa mola...
Mas temos que trocar as contantes, afinal é a constante para o nosso sistema...
Pronto! Essa é a fórmula da frequência que queríamos!