Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 61

61. Um deslizador de 500   g , com uma mola de constante elástica de 10   N / m preso a ele, encontra-se em repouso sobre um trilho de ar praticamente desprovido de atrito. A partir de uma extremidade afastada do trilho de ar, outro deslizador de 250   g é impulsionado a 120   c m / s em direção ao primeiro deslizador. Ele colide com o deslizador de 500   g e fica grudado a ele. Quais são a amplitude e o período das oscilações decorrentes?

Passo 1

Opa! E aí brother! Aqui vamos nós de novo!

Se liga só! Uma colisão completamente inelástica entre os dois planadores está acontecendo no nosso problema. A seguinte imagem abaixo mostra isso...

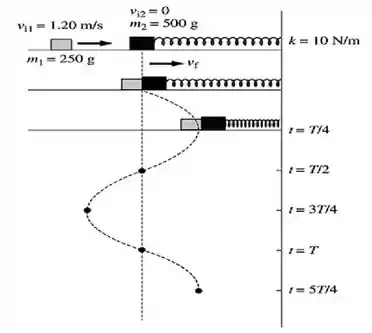
E acaba que essa colisão resulta em um movimento harmônico simples!

Passo 2

Aí já sabe o que tem que fazer, né companheiro!? Se temos uma colisão completamente inelástica, bora então, aplicar a conservação do momento angular...

p f = p i

Consideremos que os blocos estão a velocidades iniciais v i 1 e v i 2 , para m 1 e m 2 , respectivamente.

E uma vez que a colisão é completamente inelástica, então os dois blocos seguira juntos e a uma mesma velocidade v f após a colisão.

Logo, ficamos com...

p f = p i

m 1 + m 2 v f = m 1 v i 1 + m 2 v i 2

Pelo enunciado, tiramos que...

m 1 = 0,250   k g

m 2 = 0,500   k g

v i 1 = 1,20   m / s

v i 2 = 0   m / s

Desse modo, a velocidade final dos blocos será...

m 1 + m 2 v f = m 1 v i 1 + m 2 v i 2

0,750   k g v f = 0,250   k g ⋅ ( 1,20   m / s ) + ( 0,500   k g ) ( 0   m / s )

0,750   k g v f = 0,3   k g ⋅ m / s

v f = 0,3   k g ⋅ m / s 0,750   k g

v f = 0,4   m / s

Passo 3

Mas calma que ainda não terminou! Após os dois blocos se grudarem, eles entram em contato com uma mola e passam a executar um M H S

Desse modo, como o que a questão pede é a amplitude do movimento, podemos faze isso usando a conservação da energia mecânica, relacionando os momentos no qual os blocos comprimem a mola ao momento no qual estão em equilíbrio, com velocidade máxima na oscilação.

Vale lembrar que durante a compressão, o bloco está em sua amplitude máxima. Não há velocidade aí, meu camarada!

Ficamos então, com

K c o m p r e s s ã o + U c o m p r e s s ã o = K e q u i l í b r i o + U e q u i l í b r i o

1 2 k A 2 = m 1 + m 2 2 ⋅ v f 2

A 2 = ( m 1 + m 2 ) v f 2 k

A = ( m 1 + m 2 ) v f 2 k

E subsituindos os valores numéricos que temos...

A = 0,250   k g + 0,500   k g ⋅ ( 0,4   m / s ) 2 10   N / m

A = 0,110   m

Passo 4

Finalmente, para obter o período de oscilação, basta usar a fórmula abaixo para oscilação em um sistema massa-mola:

T = 2 π m k

A massa m dessa fórmula... Levando para o nosso caso, vai ser a soma de m 1 com m 2 :

T = 2 π m 1 + m 2 k

T = 2 π 0,25   k g + 0,50   k g 10   N / m

T = 2 π 0,75   k g 10   N / m

T = 1,72   s

E pronto! Terminamos aqui!

Resposta

A = 0,110   m

T = 1,72   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

65. Uma ligação molecular pode ser modelada como uma mola presa entre dois átomos que vibram em movimento harmônico simples. A FIGURA P14.65 mostra uma aproximação de MHS para a energia potencial de u
68. Em sua primeira viagem ao Planeta X , você leva consigo uma massa de 200g , uma mola de 40 cm de comprimento, uma régua e um cronômetro. Você está curioso para saber qual é a aceleração de queda l
69. A cabeça de 15g de um boneco que mexe com a cabeça oscila em MHS com freqüência de 4,0H z . a. Qual é a constante elástica da mola sobre a qual a cabeça está montada? b. Suponha que a cabeça seja
67. Uma moeda de centavo encontra-se sobre o topo de um pistão enquanto efetua um movimento harmônico simples com 4,0c m de amplitude. Se a freqüência for baixa, a moeda sobe e desce sem dificuldade.
Um objeto em MHS oscila com período de 4,0s e amplitude de 10c m . Quanto tempo transcorrerá para que o objeto se mova de x = 0,0c m para x = 6,0c m ?