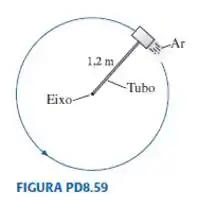
Um bloco de aço de descreve um círculo sobre uma mesa de aço, presa por um barbante de de comprimento, como mostrado na FIGURA . Ar comprimido é introduzido através do tubo e ejetado através de um bico existente na traseira do bloco, exercendo uma força de empuxo de perpendicularmente ao tubo. A máxima tensão à qual o tubo pode resistir e não se romper é de . Se o bloco parte do repouso, quantas revoluções ele completará antes que o tubo se rompa?

Olá, tudo bem?

Os dados que o problema nos dá são:

Como a mesa é de aço e o bloco também, temos uma força de atrito, cujo coeficiente é dado por .

Saca só esse diagrama de forças:

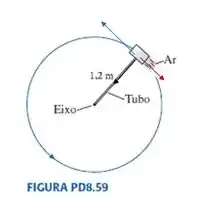
Em vermelho temos a força de atrito cinético , em azul a força de empuxo que faz o tudo se mover, e em preto temos a tensão , que é na mesma direção e sentido que a força centrípeta . Não incluí aí a força normal (perpendicular ao plano da página saindo) e a força peso (também perpendicular ao plano da página, mas entrando). Essas duas últimas tem o mesmo módulo e sentidos opostos .

Agora vamos as equações de força. Na direção radial temos:

Então daqui tiramos o valor da velocidade angular quando a tensão é máxima:

E na direção tangencial:

Daqui temos a aceleração tangencial: