Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 58
Passo 1
Fala galera, tudo bem? Vou ajudar vocês nessa aqui! Vamos lá?
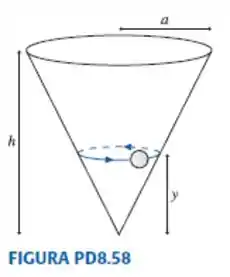
A bolinha está na parede desse cone, certo? E sabemos que a normal é perpendicular à superfície de apoio, então ela vai ter uma componente radial e vertical em relação a esse movimento circular, beleza?
Pra ficar claro o que quero dizer, vou fazer um desenho em cima da figura do livro, saca só:
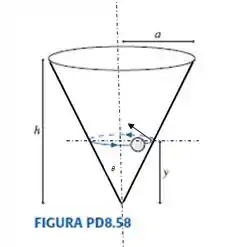
O ângulo ali do cone é o mesmo ângulo que a normal faz com a direção radial! Então na direção radial temos a componente horizontal da normal que é e que deve ser igual à força centrípeta . Já a componente vertical deve contrabalançar a força peso . Ficamos com o seguinte sistema de equações:
Passo 2
Queremos determinar o módulo da velocidade, e sabemos os valores de e , mas não sabemos de . Mas dá uma olhada com mais carinho no desenho. Não podemos usar a tangente de ? Temos o cateto oposto que seria e o adjacente que seria , então:
Passo 3
Agora vou dividir a segunda equação do nosso sistema pela primeira:
Do lado esquerdo cortamos os e ficamos com . Do lado direito cortamos as massas:
Estamos quase lá! Sabemos que , então:
Daí temos:
Agora sim! Temos a velocidade da bolinha em termos da quantidade =D. Vimos que as outras quantidades não influenciam para o módulo da velocidade, beleza?
Beleza?
Espero ter ajudado!
Vamos pra próxima?