Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 5.9 - Ex. 31
Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial . O ângulo do plano inclinado é . (a) Que distância ao longo do plano inclinado o bloco consegue atingir? (b) Quanto tempo o bloco leva para percorrer essa distância? (c) Qual é a velocidade do bloco ao chegar de volta ao ponto de partida?
Passo 1
Para iniciar essa questão precisamos ter em mente que a força resultante que age sobre um corpo é a soma de todas as forças que atuam no mesmo e está relacionada à aceleração pela definição da segunda lei de Newton:
Podemos considerar, nesta questão, que a força resultante age somente em uma direção, assim podemos aplicar a segunda lei de Newton para a componente nesta direção:
Mas essa questão não é só de lei de Newton, percebeu quando leu? Aqui precisamos usar algumas funções da cinemática de MRUV:
Nessa questão foi dado a velocidade inicial do bloco (), o ângulo do plano inclinado (), diz que o plano inclinado não tem atrito e pede a distância que o bloco percorre até parar, quanto tempo o bloco leva para percorrer esta distância e a velocidade que o bloco chega quando atinge novamente o ponto de partida.
Passo 2
Vamos iniciar fazendo o DCL para poder aplicar a segunda lei de Newton:
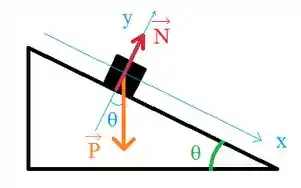
Aqui deu para visualizar melhor, né?
Vamos aplicar a segunda lei de Newton para a componente que é a componente que importa para nós, pois a componente está em equilíbrio. Assim:
Como temos dos dois lados da equação, podemos cortá-lo, portanto:
Sabendo que e , então:
Passo 3
Com a aceleração já calculada, podemos aplicar a famosa equação de Torricelli para determinar a distância percorrida pelo bloco. Para isso, manteremos o eixo definido no passo anterior:
Sabendo que , e , então:
A variação de posição foi definida de forma que o ponto que o bloco atinge seja a origem. Isso foi feito para manter o eixo definido no passo anterior. Portanto, isolando o :
Passo 4
Para determinar o tempo até atingir o ponto mais alto, aplicaremos a função da velocidade do MRUV:
Sabendo que , e , então:
Isolando o :
OBS: Lembrando que, no ponto mais alto, a velocidade é zero e que foi mantido o eixo do passo .
Passo 5
Como a aceleração para subir é a mesma para descer e a distância percorrida é a mesma, então a velocidade que o bloco chega embaixo tem mesmo módulo que a velocidade que ele inicia a subida, porém no sentido contrário. Assim:
Resposta
- ;
- ;
- .