Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 24

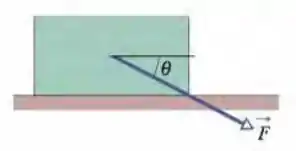
Um bloco é empurrado sobre um piso horizontal por uma força constante que é aplicada fazendo um ângulo θ para baixo (Fig. 6-19). A Fig. 6-36 mostra o módulo da aceleração α em função do coeficiente de atrito cinético μ k entre o bloco e o piso. Se a 1 = 3,0   m / s 2 , μ k 2 = 0,20 e μ k 3 = 0,40 , qual é o valor de θ ?

Passo 1

Vamos iniciar a resolução deste problema pelo DCL:

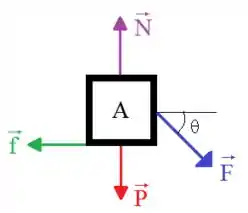
A partir da ilustração para visualizar melhor como as forças estão dispostas, podemos aplicar a segunda lei de Newton para cada eixo:

e i x o   x :       F cos ⁡ θ - f k = m a       e q . 1

e i x o   y :       N - P - F sin ⁡ θ = 0       e q . 2

Colocamos que o e i x o   y está em equilíbrio, pois o movimento ocorre exclusivamente no e i x o   x .

Além disso, para resolver esta questão é preciso lembrar que podemos calcular a força de atrito cinético usando a seguinte relação:

f k = μ k N       e q . 3

Passo 2

Vamos começar determinar o valor de f k , para tanto, é preciso usar a e q . 2 para determinar o valor da normal:

N = m g + F sin ⁡ θ

Substituindo essa expressão na e q . 3 :

f k = μ k m g + μ k F sin ⁡ θ       e q . 4

Passo 3

Agora, vamos substituir a e q . 1 na e q . 4 para completar a equação para substituir os valores dado no enunciado que pode ser extraído no gráfico:

F cos ⁡ θ - μ k m g - μ k F sin ⁡ θ = m a       e q . 5

De acordo com o gráfico, a = 3   m / s 2 para μ k = 0 , assim:

F cos ⁡ θ = 3 m

Rearranjando esta expressão:

F m = 3 cos ⁡ θ     e q . 6

Podemos extrair do gráfico também os pontos a = 0 para μ k = 0,20 , assim, substituindo na e q . 5 :

F cos ⁡ θ - 0,2   m g - 0,2   F   s i n θ = 0

F cos ⁡ θ - μ k sin ⁡ θ = 0,2 × 9,8 × m

F m = 1,96 cos ⁡ θ - 0,2 sin ⁡ θ       e q . 7

Passo 4

Igualando a e q . 6 e a e q . 7 :

3 cos ⁡ θ = 1,96 cos ⁡ θ - 0,2 sin ⁡ θ

cos ⁡ θ cos ⁡ θ - 0,2 sin ⁡ θ cos ⁡ θ = 1,96 3

1 - 0,2 tan ⁡ θ = 0,65

Isolando tan ⁡ θ :

1 - 0,65 0,2 = tan ⁡ θ

Isolando o θ :

θ = tan - 1 ⁡ 1 - 0,65 0,2 = 60 °

Resposta

θ = 60 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma cômoda com uma massa de 45k g , incluindo as gavetas e as roupas, está em repouso sobre o piso. (a) Se o coeficiente de atrito estático entre a cômoda e o piso é 0,45 , qual é o módulo da menor fo
Em um jogo de shuffleboard improvisado, estudantes enlouquecidos pelos exames finais usam uma vassoura para movimentar um livro de cálculo no corredor do dormitório. Se o livro de 3,5k g adquire uma v
Um bloco de 2,5k g está inicialmente em repouso em uma superfície horizontal. Uma força horizontal P de módulo 6,0N e uma força verticalP são aplicadas ao bloco ( F i g .6 - 17 ) . Os coeficientes de
Um bloco é lançado para cima, com velocidade de 5 m/s, sobre uma rampa de 45 ° de inclinação. O coeficiente de atrito cinético entre o bloco e a rampa é de 0,3. a) Qual é a distância máxima atingida p
Brincando nas vizinhaças do canteiro de obras de uma estrada, uma criança cai em uma encosta que faz um ângulo de 35 ° com a horizontal. Enquanto a criança escorrega encosta abaixo, sofre uma aceleraç