Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 94
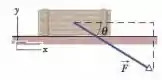
Na Fig. 6-58, uma força é aplicada a um caixote de massa m que repousa em um piso; o coeficiente de atrito estático entre o caixote e o piso é . O ângulo é inicialmente , mas é gradualmente aumentado, de modo que a direção da força gira no sentido horário. Durante a rotação, a intensidade da força é continuamente ajustada para que o caixote permaneça na iminência de se mover. Para , (a) plote a razão em função de e (b) determine o ângulo para o qual a razão se toma infinita. (c) Se o piso é lubrificado, o valor de Oinr aumenta, diminui ou permanece inalterado? (d) Qual é o valor de para ?
Passo 1
Bom pessoal , nós sabemos que a componente horizontal de empurra o caixote, enquanto a componente vertical aumenta a força de atrito, ao aumentar a força normal. Aplicando a Segunda Lei de Newton nas direções, temos:
O fato do caixote estar na iminência de se mover , significa que a força de atrito estático está em seu valor máximo , sendo assim :
Combinando as três equações, obtemos :
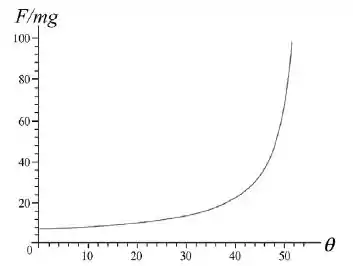
A figura abaixo mostra um gráfico da razão em função de (com em graus).
Até aqui beleza, pessoal? Bora continuar então!
Passo 2
A gente sabe que a razão se torna infinita quando o denominador é nulo . Nesse caso , o denominador da expressão de em função de se anula para :
Logo ,
Para , temos que :
Passo 3
Bom pessoal , se o piso for lubrificado, o coeficiente de atrito estático será menor , e analisando a fórmula achada no item anterior percebemos que quanto menor maior é valor de , sendo assim , o ângulo será maior que o valor calculado no item (b).
Passo 4
Para .temos que :
.
Resposta
Respectivamente :
De boa pessoal ???? Bora resolver mais questões então