Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.1 - Ex. 2
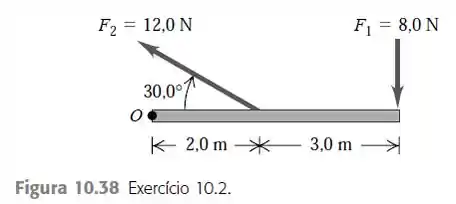
Calcule o torque resultante em torno de um ponto O para as duas forças aplicadas mostradas na Figura 10.38. A barra e as forças estão sobre o plano da página.
Passo 1
Eaee, belezinha??? Bom... queremos calcular o torque resultante em torno de um ponto O para as duas forças aplicadas mostradas na figura abaixo:
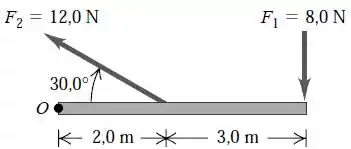
Para isso, sabemos que o torque é dado pela produto entre a força e o braço de alavanca :
Com .
Nesse sentido, para resolvermos esse probleminha, nós vamos adicionar os dois torques para calcular o torque total.
Vamos considerar que os torques no sentido anti-horário sejam positivos, ok?
Bora lá! 😉
Passo 2
Dessa forma temos que o Torque 1 é:
Com:
Assim,
Passo 3
E o torque 2 é:
Com:
Assim,
Passo 4
E então, a somando-os, temos que:
Portanto, o torque é de , no sentido horário. 😉
Resposta
O torque é de , no sentido horário.