Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 108

Um bloco de madeira (massa m ) está ligado a duas molas sem massa, como mostrado na Figura 7-59. Cada mola tem um comprimento frouxo L e uma constante de força k . (a) Se o bloco é deslocado de uma distância x , como mostrado, qual é a variação da energia potencial armazenada nas molas? (b) Qual é a magnitude da força que puxa o bloco de volta à sua posição de equilíbrio? (c) Usando um programa de planilha eletrônica, ou uma calculadora gráfica, faça um gráfico da energia potencial U como função de x para 0 ≤ x ≤ 0,20   m . Suponha k = 1   N / m , l = 0,10   m e m = 1,0   k g . (d) Se o bloco é deslocado de uma distância x = 0,10   m e liberado, qual é sua rapidez quando passa pelo ponto de equilíbrio? Suponha o bloco sobre uma superfície sem atrito.

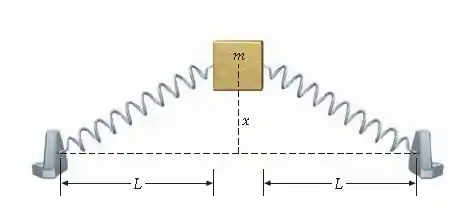
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O diagrama de corpo livre da situação está exposto abaixo:

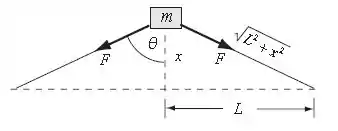
Com o auxílio da figura, podemos expressar a variação da energia potencial. Temos que:

∆ U = 2 1 2 k ∆ L 2

∆ U = k ∆ L 2

Podemos identificar no diagrama que:

∆ L = L 2 + x 2 - L

Logo:

∆ U = k L 2 + x 2 - L 2

Passo 2

Item (b):

A força resultante agindo no bloco é dada por:

F r e s = 2 F cos ⁡ θ

F r e s = 2 k ∆ L cos ⁡ θ

F r e s = 2 k ∆ L x L 2 + x 2

Substituindo ∆ L , temos:

F r e s = 2 k ( L 2 + x 2 - L ) x L 2 + x 2

Temos que:

F r e s = 2 k x 1 - L L 2 + x 2

Passo 3

Item (c):

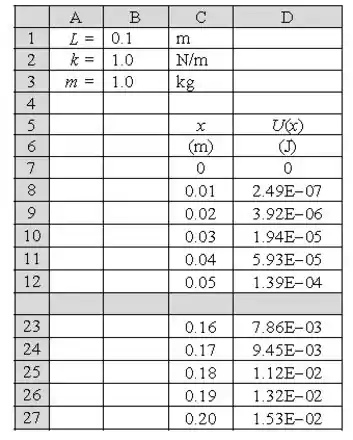
Abaixo está a figura da planilha onde podemos ver o comportamento da Energia Potencial ao variarmos x .

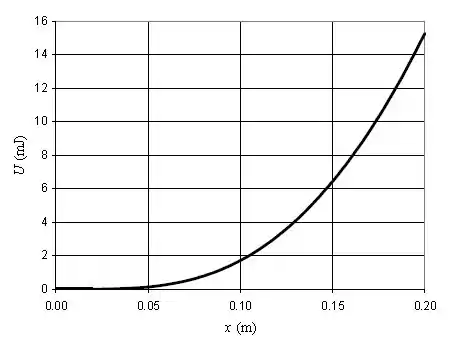
A partir dos dados, foi possível plotar o seguinte gráfico:

Passo 4

Item (d):

Aplicando Conservação da Energia Mecância, temos que:

K = ∆ U

1 2 m v 2 = ∆ U

v = 2 ∆ U m

Substituindo as equações, temos:

v = 2 k L 2 + x 2 - L 2 m

v = L 2 + x 2 - L 2 k m

Substituindo os valores, temos:

v = 0,1   m 2 + ( 0,1   m ) 2 - 0,1   m 2 ⋅ ( 1   N / m ) 1   k g

v = 0,0586   m / s

v = 58,6   c m / s

Resposta

a ) ∆ U = k L 2 + x 2 - L 2

b ) F r e s = 2 k x 1 - L L 2 + x 2

d ) v = 58,6   c m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

31. A energia potencial de um corpo de 4,0K g restrita ao eixo x é dada por U = 3 x 2 - x 3 para x ≤ 3,0m e U = 0 para x ≥ 3,0m , onde U está em joules e x está em metros, e a única força que atua sob
30. A força resultante que atua sobre um corpo restringido ao eixo x , é dada por F x x = x 3 - 4 x . (A força está em newtons e x em metros.) Localize as posições de equilíbrio instável e estável. Mo
33. Uma barra reta de massa desprezível está montada sobre um pivô sem atrito, como mostrado na figura 7-38. Blocos de massa m 1 e m 2 estão presos à barra, nas distânica l 1 e l 2 .a) Escreva uma exp
35. Você projetou um relógio bem original, mostrado na Figura 7-40. Sua preocupação é que ele ainda não esteja pronto para o mercado, pela possibilidade de apresentar uma configuração de equilíbrio in
Uma bola de gude move-se ao longo do eixo Ox. A energia potencial �� indicada na Figura 7.28. a) Para quais valores de x indicados no gráfico a força é igual a zero? b) Para quais valores de x indicad