Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 35

35. Você projetou um relógio bem original, mostrado na Figura 7-40. Sua preocupação é que ele ainda não esteja pronto para o mercado, pela possibilidade de apresentar uma configuração de equilíbrio instável. Você decide aplicar seu conhecimento sobre energia potencial e condições de equilíbrio para analisar a situação. O relógio (massa m) é suspenso por dois cabos leves que passam por duas polias sem atrito, de diâmetro desprezível, que estão ligadas a contrapesos de massa M , cada um.

(a) Determine a energia potencial do sistema como função da distância y .

(b) Determine o valor de y para o qual a energia potencial do sistema é mínima.

(c) Se a energia potencial é mínima, o sistema está em equilíbrio. Aplique a segunda lei de Newton ao relógio e mostre que ele está em equilíbrio (as forças sobre ela somam zero) para o valor de y obtido para a parte (b).

(d) Por fim, determine se você conseguirá comercializar a invenção: o ponto de equilíbrio é estável ou instável?

Passo 1

(a) Seja L o comprimento total de um cabo e considerando que o zero de energia potencial gravitacional esteja no topo das polias, vamos expressar a energia potencial do sistema, como a soma da energia potencia do relógio U R e dos contrapesos U C P :

U ( y ) = U R + U C P

Substituímos então as fórmulas de cada tipo de energia. Os contrapesos, dentro do referencial do nosso sistema vão estar a uma altura ( L - y 2 + d 2 ) :

U y = - m g y - 2 M g L - ( y 2 + d ² )

Passo 2

b) Podemos encontrar o valor de y para o qual a energia potencial do sistema é mínima, derivando U y   em relação a y   e definindo essa derivada igual a zero. Vai dar trabalho, mas vamos lá! Mão na massa!

U y = - m g y - 2 M g L - ( y 2 + d ² )

Queremos d U / d y   :

d U d y = d d y - m g y - 2 M g L - ( y 2 + d ² )

d U d y = d d y - m g y - d d y 2 M g L - ( y 2 + d ² )

d U d y = - m g - 2 M g d d y L - ( y 2 + d ² )

d U d y = - m g + 2 M g d d y ( y 2 + d ² )

d U d y = - m g + 2 M g y ( y 2 + d ² )

d U d y = - m g + 2 M g y ( y 2 + d ² )

Iguala-se d U / d y   a zero:

- m g + 2 M g y ( y 2 + d ² ) = 0

2 M g y ( y 2 + d ² ) = m g

2 M y ( y 2 + d ² ) = m

( 2 M y ) 2 = m ( y 2 + d ² ) 2

4 M 2 y 2 = m 2 ( y 2 + d ² )

y 2 4 M 2 - m 2 = m ² d ²

y = d m ² 4 M 2 - m 2

Agora falta realizar o teste da segunda derivada! Meu Deus! Quanto trabalho! Mas vamos lá!

Queremos d ² U / d y ²

d 2 U d y 2 = d d y - m g + 2 M g y ( y 2 + d ² )

d 2 U d y 2 = d d y 2 M g y ( y 2 + d ² )

d 2 U d y 2 = 2 M g d d y y ( y 2 + d ² )

d 2 U d y 2 = 2 M g d d y ( y 2 + d ² ) - y ² ( y 2 + d ² ) ( y 2 + d ² ) 2

d 2 U d y 2 = 2 M g d ² ( y 2 + d ² ) 3 / 2  

Pera! Pera! Pera! Não acredito. A única parte pertencente a y na segunda derivada é justamente no denominador, onde ele está elevado ao quadrado. Isso quer dizer, que para qualquer y , a segunda derivada sempre vai ser maior que 0 . Encontramos um ponto de mínimo.

Logo, a menor energia potencial ocorre em y = d m ² 4 M 2 - m 2   .

Passo 3

c) Tracemos o diagrama de corpo livre para o relógio:

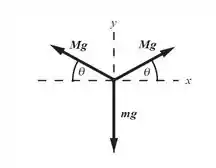
De cara já sabemos que no eixo x , as duas forças M g , que estão em sentidos opostos, vão se anular. Vamos agora, calcular o somatório das forças no eixo y considerando a situação de equilíbrio:

∑ F y = 0

m g - 2 M g sen ⁡ θ = 0

m g = 2 M g sen ⁡ θ

sen ⁡ θ = m 2 M

Mas olhando bem a figura do enunciado, vemos que sen ⁡ θ pode ser escrito também como:

sen ⁡ θ = y y 2 + d 2

Agora, obtemos a relação que queríamos:

sen ⁡ θ = y y 2 + d 2 = m 2 M

Essa relação é exatamente igual a desenvolvida no cálculo da primeira derivada em U , lá na letra b, onde confirmou-se que a energia potencial é mínima. Logo, o sistema está em equilíbrio.

Passo 4

d) O relógio pode ser comercializado. Este é um ponto de equilíbrio estável. Se o relógio estiver deslocado para baixo, θ aumenta, levando a uma maior força ascendente no relógio. Da mesma forma, se o relógio fordeslocado para cima, a força resultante dos cabos diminui. Por esse motivo, o relógio será puxado para trás em direção ao ponto de equilíbrio, caso seja deslocado para longe deste.

Resposta

a) U y = - m g y - 2 M g L - ( y 2 + d ² )  

b) y = d m ² 4 M 2 - m 2

c) sen ⁡ θ = y y 2 + d 2 = m 2 M

d) O relógio pode ser comercializado. Trata-se de um ponto de equilíbrio estável.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

36 . || Um cubo de gelo bem liso desliza dentro de um tubo horizontal liso com 20c m de diâmetro interno, descrevendo uma trajetória em um plano vertical. Na parte mais inferior do tubo, a velocidade
35 . || O Frisbee de seu amigo ficou preso em uma árvore a 16m acima do solo. Você deseja desalojá-lo acertando-o com uma pedra. O brinquedo está firmemente preso à árvore, de modo que você percebe qu
42 . || Um pacote de massa m é liberado a partir do repouso do galpão de armazenamento de uma loja e desliza sem atrito por uma rampa até o caminhão estacionado. Infelizmente, o motorista estacionou o
43 . || Um cubo de granito de 100g desce deslizando por uma rampa sem atrito e com 40 ° de inclinação. Na base da mesma, exatamente quando o cubo entra na superfície horizontal de uma mesa, ele colide
40 . || Uma bola de borracha de 500g é solta de uma altura de 10m e sofre uma colisão perfeitamente elástica com a Terra. a . Qual é a velocidade da Terra após a colisão? Considere que a Terra esteja