Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 5.3 - Ex. 57
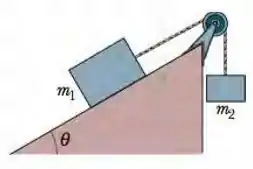
Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig. 5-52). Quais são (a) o módulo da aceleração de cada bloco, (b) o sentido da aceleração do bloco que está pendurado e (c) a tensão da corda?
Passo 1
Este é um problema de aplicação da segunda lei de Newton (), usando também o conceito da terceira lei de Newton (ação e reação).
Para questões como essa, é bastante interessante sempre fazer o DCL de cada corpo:
Com essa ilustração, podemos entender melhor como as forças estão atuando nos blocos. Além disso, é importanta lembrar que como a polia é ideal as tensões no bloco e são de mesmo módulo.
O movimento dos blocos é dado em conjunto, portanto, a aceleração de ambos deve ser a mesma, show?
Passo 2
Vamos inciar escrevendo a segunda lei de Newton para o eixo do bloco e vamos supor que o bloco suba o plano inclinado, caso essa afirmação seja falsa, o módulo da aceleração que encontraremos será negativo.
Substituindo os valores conhecidos e isolando o :
Passo 3
Agora vamos fazer a mesma coisa para o eixo do bloco , lembrando que, como consideramos que o bloco está subindo, então o bloco está descendo e, por isso, a aceleração é negativa. Assim:
Isolando o e substituindo os valores conhecidos:
Passo 4
Igualando a e a :
Isolando o :
Como, encontramos a aceleração positiva, então nossa suposição foi correta e, portanto, o bloco está acelerado para baixo.
Passo 5
Para determinar a tensão na corda, vamos usar a
Resposta
- ;
- ;
- .