Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 2.Problemas Adicionais - Ex. 90
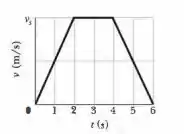
Uma partícula parte da origem em e se move no sentido positivo do eixo . O gráfico da velocidade da partícula em função do tempo é mostrado na Fig. 2-43; a escala vertical é definida por . (a) Qual é a coordenada da partícula em ? (b) Qual é a velocidade da partícula em ? (c) Qual é a aceleração da partícula em ? (d) Qual é a velocidade média da partícula entre e ? (e) Qual é a aceleração média da partícula entre e ?
Passo 1
Para começar vamos lembrar a definição de deslocamento:
,
sem esquecer que a integral é a área da função que estamos integrando.
O exercício nos deu o gráfico da velocidade. Então, para calcular o deslocamento, ou a posição da partícula em (), basta calcularmos a área do gráfico de até .
Para resolução de problemas como este, o macete é separar o gráfico em figuras, as quais as fórmulas de área são conhecidas. A fórmula que você precisa saber para resolver este exercício é:
Então, separando o gráfico acima, ficamos com:
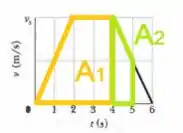
Primeira figura (trapézio laranja):
Segunda figura (trapézio verde):
Portanto, para encontrar a posição da partícula no instante somamos as áreas calculadas acima:
Passo 2
Podemos retirar a velocidade no instante olhando diretamente o gráfico dado. Como o enunciado diz que dois retângulos equivalem a , então um retângulo equivale a .
Portanto, como no instante o gráfico da velocidade intercepta o primeiro retângulo da grade, a velocidade neste instante é:
Passo 3
Para resolver esta etapa vamos lembrar a relação da velocidade e da aceleração:
sem esquecer que a inclinação da função velocidade.
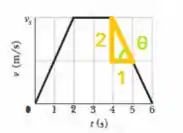
Logo, para determinar a aceleração no instante precisamos determinar o coeficiente angular da reta, ou seja, a tangente de :
Passo 4
Para calcular a velocidade média precisamos ter em mente que nem sempre a velocidade média e a velocidade instantânea serão numericamente iguais. Este problema, por exemplo, a velocidade média e a velocidade instantânea não são iguais!
Então, vamos definir primeiro o que é velocidade média:
Portanto, para calcular a velocidade média da partícula entre e precisamos calcular o deslocamento nesse período de tempo e para calcular esse deslocamento vamos ter que calcular a área do gráfico entre estes instantes:
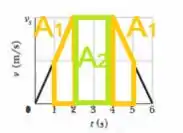
Calculando as áreas e aproveitando a simetria da figura:
Primeira figura (trapézio laranja):
Segunda figura (retângulo verde):
Portanto, o deslocamento total entre os instantes e é:
Usando a definição de velocidade média, temos:
Passo 5
Relembrando, inicialmente, a definição de aceleração média:
Como a velocidade no instante é igual a velocidade no instante , então a variação da velocidade é zero e, portanto:
Resposta
- ;
- ;
- ;
- ;
- .