Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 64
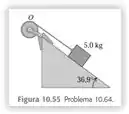
Um bloco de massa desliza para baixo de uma superfície horizontal inclinada a 36,9º com a horizontal (Figura 10.55). O coeficiente de atrito cinético é 0,25. Um fio amarrado ao bloco é enrolado em torno de um volante que gira em torno de um eixo passando em O.
O volante possui massa de 25,0 kg e momento de inércia de em relação ao eixo de rotação. O fio puxa a roda sem deslizar a uma distância perpendicular ao eixo igual a 0,200 m.
a) Qual é a aceleração do bloco para baixo do plano?
b) Qual é a tensão no fio?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte figura que representa um plano inclinado:
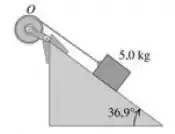
O coeficiente de atrito cinético é .
Um fio amarrado ao bloco é enrolado em torno de um volante que gira em torno de um eixo passando em O.
O volante possui massa de e momento de inércia de em relação ao eixo de rotação.
O fio puxa a roda sem deslizar a uma distância perpendicular ao eixo igual a .
Queremos calcular a aceleração do bloco para baixo do plano. Para isso, precisaremos da seguinte expressão (Segunda Lei de Newton):
Onde é força, é a massa e é a aceleração.
Também queremos calcular a tensão do fio. Para isso, precisaremos da seguinte expressão:
Onde é o torque, é o momento angulae e é a aceleração angular.
Passo 2
De início, o problema nos pede a aceleração do bloco, certo?
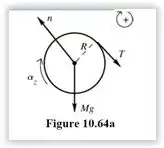
Fazendo o diagrama do volante para expormos as forças atuantes, nos resta:
Passo 3
Aplicando , como as forças normal e peso agem no eixo, então o torque é zero. Certo? Assim, dá para substituirmos
Lembrando que , onde é aceleração do bloco, a nossa incógnita. Então
Agora vamos guardar essa relação e analisar o bloco. :D
Passo 4
Para o bloco se movimentando de modo translacional, temos
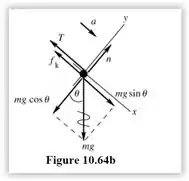
Aplicando para o eixo y
Para o eixo x, a força de atrito é
Substituindo T daquela relação que a gente guardou,
Logo,
Passo 5
Na letra b, precisamos calcular a tensão no fio. Usando novamente aquela fórmula que tínhamos como guardada,
Resposta
a) ;
b) .