Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 29
|| Partindo do repouso, um de de que é diâmetro leva para atingir sua velocidade normal de operação, que é de . Considere que a aceleração angular seja constante. O momento de inércia do disco é de .
Que valor de torque deve ser exercido sobre o disco?
Quantas revoluções ele fará até atingir a velocidade final?
Passo 1
Um desenho é:
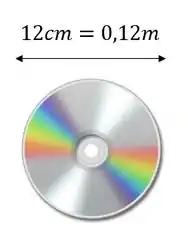
Temos:
Passo 2
Que valor de torque deve ser exercido sobre o disco?
Podemos encontrar a aceleração angular:
Com isso, podemos achar o Torque:
Passo 3
Quantas revoluções ele fará até atingir a velocidade final?
Podemos usar a fórmula de cinemática de um movimento circular para achar:
Resposta
Exercícios de Livros Relacionados
O volante de certa máquina possui momento de inércia igual a 2,50k g ⋅ m 2 em torno do seu eixo de rotação. Qual é o torque constante necessário para que, partindo do repouso, sua velocidade angular a
Uma casca esférica uniforme de 8,40 kg e 50,0 cm de diâmetro possui quatro pequenas massas de 2,0 kg presas à superfície externa e igualmente espaçadas entre si. Esse sistema está girando em torno de
Um balde com água de 15,0k g é suspenso por uma corda enrolada em torno de um sarilho, constituído por um cilindro sólido com diâmetro de 0,300m e massa igual a 12,0k g . O cilindro é pivotado sobre u
A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de 225 g e diâmetro de 3,0 cm. Ela está girando em torno de um eixo com atrito desprezível que passapelo seu centro, mas e
Um cilindro maciço e uniforme com massa de 8,25k g e diâmetro de 15,0c m está girando a 220r p m sobre um eixo delgado e de atrito desprezível, que passa ao longo do eixo de cilindro. Você projeta um