Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 70

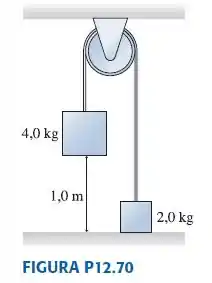
Os dois blocos da FIGURA P12.70 estão ligados por uma corda de massa desprezível que passa por uma polia. Esta tem 12 cm de diâmetro e uma massa de 2,0 kg. Quando a polia gira, o atrito com o eixo exerce um torque de módulo igual a 0,50 N m. Se os blocos forem liberados do repouso, quanto tempo decorrerá até que o bloco de 4,0 kg atinja o piso?

Passo 1

A polia é um corpo rotativo rígido. Também assumimos que a polia tem a distribuição de massa de um disco e que a corda não desliza.

Vamos visualizar:

Passo 2

Agora vamos desenhar o diagrama de corpo livre de cada bloco:

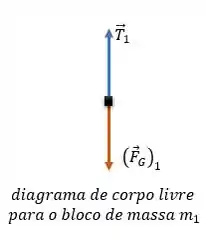
Como a polia não é sem massa e sem atrito, a tensão na corda em ambos os lados da polia não é a mesma.

Passo 3

Então, vamos resolver. A aplicação da segunda lei de Newton a m 1 e m 2 e a polia produz as três equações:

T 1 - F G 1 = m 1 a 1 - F G 2 + T 2 = m 2 a 2 T 2 R - T 1 R - 0,50   N ⋅ m = I α

Note que,

- a 2 = a 1 = a , I = 1 2 m p o l i a R 2 ,e α = a R

e então as equações acima simplificam para:

T 1 - m 1 g = m 1 a

m 2 g - T 2 = m 2 a

T 2 - T 1 = 1 2 m p o l i a R 2 a R 1 R + 0,50   N ⋅ m R = 1 2   m p o l i a a + 0,50   N ⋅ m 0,060   m

Passo 4

Adicionando essas três ultimas questões:

m 2 - m 2 g = a m 1 + m 2 + 1 2   m p o l i a + 8,333   N

Isolando a :

a = m 2 - m 1 g - 8,333   N m 1 + m 2 + 1 2   m p o l i a = ( 4   k g - 2   k g ) ( 9,8   m / s 2 ) - 8,333   N 2   k g + 4   k g + ( 2   k g / 2 ) = 1,610   m / s 2

Passo 5

Agora podemos usar a cinemática para encontrar o tempo gasto pelo bloco de 4 kg para chegar ao chão:

y 1 = y 0 + v 0 ( t - t 0 ) + 1 2 a 2 t - t 0 2

⇒ 0 + 1   m + 0 + 1 2 ( - 1,610   m / s 2 ) ( t 1 - 0 s ) 2

⇒ t 1 = 2 ⋅ ( 1 m ) 1,610   m / s 2 = 1,11   s

Resposta

1,11   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo indicado na Figura 10.53 é usado para elevar um engradado de suprimentos do depósito de um navio. O engradado possui massa total de 50 kg. Uma corda é enrolada em um cilindro de madeira qu
Dois pesos estão ligados por uma corda muito leve e flexível, que passa sobre uma polia de 50,0m com atrito desprezível e raio de 0,300m . A polia é um disco maciço e uniforme e está suspenso por um g
Dois discos metálicos, um com raio R 1 =2,50c m e massa M 1 =0,80k g e outro com raio R 2 =5,0c m e massa M 2 =1,60k g , são unidos por uma solda e montados sobre um eixo sem atrito passando no centro
A porta sólida de madeira de um ginásio tem largura de 1,0 m e altura de 2,0 m, sua massa total é igual a 35,0 kg e ela possui uma articulação em um dos seus lados. A porta está abertae em repouso qua
Calcule o torque resultante em torno de um ponto O para as duas forças aplicadas mostradas na Figura 10.38. A barra e as forças estão sobre o plano da página.