Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 19
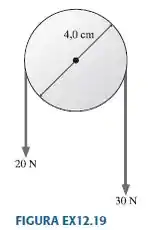
Na FIGURA EX12.19, qual é o torque resultante em torno do eixo indicado?
Passo 1
Olá, tudo bem? Vamos primeiro identificar como se calcula o torque de alguma coisa:
O que chamamos de torque é uma grandeza vetorial e em termos do seu módulo temos:
Aqui temos que é a distância entre a linha de atuação da força e o eixo de rotação. No nosso caso o eixo de rotação se encontra no centro do disco, então a distância entre ele e as duas forças é igual ao raio do disco que vale .
Passo 2
A linha de atuação das duas forças é tangente ao círculo, como você pode ver na figura do problema. Então podemos fazer um desenho dos vetores ’s para cada uma das forças, saca só:
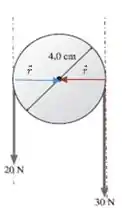
O ângulo formado entre as linhas pontilhadas e os vetores é .
Agora precisamos determinar a orientação das rotações. Vou pedir para você me ajudar nessa aqui: pegue um lápis e coloque ao longo do vetor vermelho e segure ele pela ponta esquerda, bem como se os seus dedos fossem o eixo de rotação e o lápis o braço de alavanca. Agora com a outra mão empurre a outra ponta do lápis (ponta direita) na mesma direção que a força de está fazendo, ou seja, vertical para baixo.
Agora observe o movimento que é formado. Ele é uma rotação no sentido horário ou anti-horário? Horário não é? Então taí a resposta para o sentido da rotação produzida por essa força! Rotações no sentido horário são negativas, enquanto que rotações no sentido anti-horário são positivas!
Você pode repetir esse exercício para a outra força. Você deverá segurar o lápis com a mão direita, a fim de que a ponta esquerda fique livre dessa vez. A força de é vertical para baixo, e produz uma rotação no sentido anti-horário.
Passo 3
Por fim, vamos juntar todas as informações dos passos anteriores e calcular o torque resultante. Como temos mais de uma força produzindo rotação nesse corpo, então o torque resultante será a soma dos torques:
Os dois braços de alavanca são iguais e valem , a força que produz torque positivo vale , e a força que produz torque negativo vale . O ângulo entre o braço de alavanca e a linha de atuação de força é , como já mencionei antes. Agora é só aplicar a fórmula:
Espero ter ajudado!
Vamos pra próxima?