Um bloco de massa deslizando sobre uma mesa sem atrito está preso a um fio que passa por um pequeno furo através do centro da mesa. O bloco desliza com rapidez em um círculo de raio . Determine (a) a quantidade de movimento angular do bloco, (b) a energia cinética do bloco e (c) a tensão no fio. (d) Um estudante, sob a mesa, puxa agora lentamente o fio para baixo. Qual é o trabalho necessário para reduzir o raio do círculo de para ?
Passo 1
(a) Vamos calcular o momento angular sabendo que a velocidade do bloco é perpendicular ao vetor posição que liga o centro da mesa ao bloco:
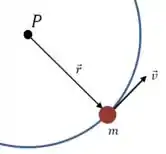
E nesses casos, sabemos que o momento angular pode ser escrito como:
Passo 2
(b) Já que temos a rapidez do bloco, e a massa , a energia cinética é simplesmente:
Passo 3
(c) A tensão no fio deve cumprir o papel de resultante centrípeta que mantém a trajetória circular de raio :
E lembrando da fórmula para a força centrípeta:
Passo 4
(d) Agora queremos calcular o trabalho necessário para reduzir o raio do círculo pela metade. Sabemos que o trabalho é igual à variação de energia cinética:
E para facilitar o cálculo podemos escrever a energia cinética em termos do momento angular:
Como o torque da força exercida pelo estudante através do fio é nula (já que , e nesse caso é paralelo a ), então o momento angular é conservado:
Quando o raio da trajetória circular é , o momento de inércia é:
E quando o raio é reduzido pela metade:
Substituindo isso na nossa equação:
E agora é só substituir com o que calculamos no passo :
Resposta
(a) .
(b) .
(c) .
(d) .